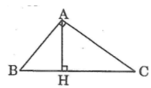
Hãy vẽ đường cao AH của hình tam giác ABC trong mỗi trường hợp sau:
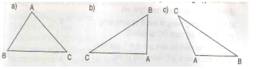
Hãy vẽ đường cao AH của hình tam giác ABC trong mỗi trường hợp sau:
Hướng dẫn:
- Đặt một cạnh góc vuông của ê-ke trùng với đường thẳng BC
- Trượt ê-ke theo đường thẳng để cạnh góc vuông còn lại của ê-ke gặp điểm A, vạch đường cao AH theo cạnh đó…
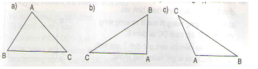
Vẽ đường cao AH của tam giác ABC trong mỗi trường hợp sau:
Cho tam giác ABC vuông tại A, đường cao AH. Giải bài toán trong mỗi trường hợp sau: Cho AH = 16, BH = 25. Tính AB, AC, BC, CH
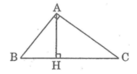
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: A H 2 = B H . C H
⇒ CH = 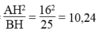
BC = BH + CH = 25 + 10,24 = 35,24
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A
B
2
=
B
H
.
B
C
⇒ AB = ![]()
≈ 29,68
A C 2 = H C . B C
⇒ AC = ![]() ≈ 18,99
≈ 18,99
Cho tam giác ABC vuông tại A, đường cao AH. Giải bài toán trong mỗi trường hợp sau: Cho AB = 12, BH = 6. Tính AH, AC, BC, CH
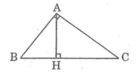
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A
B
2
=
B
H
.
B
C
⇒ BC = ![]() = 24
= 24
CH = BC – BH = 24 – 6 = 18
Theo hệ thức liên hệ giữa các cạnh góc vuông và hình chiếu, ta có:
A
C
2
=
H
C
.
B
C
⇒ AC = ![]() ≈ 20,78
≈ 20,78
Theo hệ thức liên hệ giữa đường cao và hình chiếu cạnh góc vuông, ta có:
A
H
2
=
H
B
.
B
C
⇒ AH = ![]()
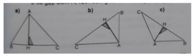
Vẽ đường cao AH của hình tam giác ABC. Hãy chọn cách vẽ đúng:
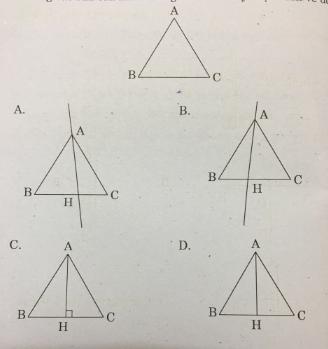
A. hình A
B. hình B
C. hình C
D. hình D
cho tam giác ABC vuông tại A, đường cao AH. Gọi E,F lần lượt là hình chiếu của H trên cạnh AB,AC.
a. Trong trường hợp AB=6, AC=8, hãy tính BC, AH, Sin b
b. Chứng minh BE.BA + AF.AC = AB2
Lời giải:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm)
$AH=2S_{ABC}:BC=AB.AC:BC=6.8:10=4,8$ (cm)
$\sin B = \frac{AC}{BC}=\frac{8}{10}=\frac{4}{5}$
b.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
$BE.BA=BH^2$
$AF.AC=AH^2$
$\Rightarrow BE.BA+AF.AC=BH^2+AH^2=AB^2$ (đpcm)
a. - Áp dụng hệ thức về cạnh và đường cao trong Δ vuông vào ΔABC vuông tại A ta có :
\(AH=\sqrt{CH.BH}=\sqrt{2.4}=2\sqrt{2}\) ( Đ.lý 2 )
- Áp dụng đ.lý Pytago vào \(\Delta AHB\perp H\) ta có :
\(AB=\sqrt{AH^2+BH^2}=\sqrt{\left(2\sqrt{2}\right)^2+4^2}=2\sqrt{6}\)
- \(BC=2+4=6\)
- Theo đ.lý Pytago :
\(AC=\sqrt{BC^2-AB^2}=\sqrt{6^2-\left(2\sqrt{6}\right)^2}=2\sqrt{3}\)
b. - Áp dụng hệ thức...trong Δ vuông ABC ta có :
+ \(BC=\dfrac{AB^2}{BH}=\dfrac{12^2}{6}=24\) ( Đ.lý 1 )
\(\Rightarrow CH=BC-BH=24-6=18\)
+ \(AH=\sqrt{BH.CH}=\sqrt{6.18}=6\sqrt{3}\) ( Đ.'ý 2 )
- Theo đ.lý Pytago ta có :
\(AC=\sqrt{BC^2-AB^2}=\sqrt{24^2-12^2}=12\sqrt{3}\)
a, BC = BH+HC
*\(AB=\sqrt{BH.BC}=\sqrt{4.8}=\sqrt{32}\)
*\(AC=\sqrt{HC.BC}=\sqrt{2.8}=4\)
*\(AH=\sqrt{BH.HC}=\sqrt{4.2}=\sqrt{8}\)
b,Theo định lý pytago ta có:
\(AH=\sqrt{AB^2-BH^2}=\sqrt{12^2-6^2}=6\sqrt{3}\)
*\(BC=\dfrac{AB^2}{BH}=\dfrac{12^2}{6}=2\)
*\(CH=BC-BH=24-6=18\)
\(AC=\sqrt{HC.BC}=\sqrt{18.24}=12\sqrt{3}\)
a, BC = BH+HC
*\(AB=\sqrt{BH.BC}=\sqrt{4.8}=\sqrt{32}\)
*\(AC=\sqrt{HC.BC}=\sqrt{2.8}=4\)
*\(AH=\sqrt{BH.HC}=\sqrt{4.2}=\sqrt{8}\)
b,Theo định lý pytago ta có:
\(AH=\sqrt{AB^2-BH^2}=\sqrt{12^2-6^2}=6\sqrt{3}\)
*\(BC=\dfrac{AB^2}{BH}=\dfrac{12^2}{6}=2\)
*\(CH=BC-BH=24-6=18\)
\(AC=\sqrt{HC.BC}=\sqrt{18.24}=12\sqrt{3}\)
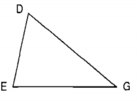
Vẽ
a) Đường cao AH của hình tam giác ABC; tam giác DEG
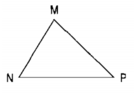
b) Đường cao EI của hình tam giác MNP
c) Đường cao PK của hình
a) Đường cao AH của hình tam giác ABC; tam giác DEG
b) Đường cao EI của hình tam giác MNP
c) Đường cao PK của hình
Cho tam giác ABC vuông tại A. Kẻ đường cao AH. Tính sinB, sinC trong mỗi trường hợp sau (làm tròn đến chữ số thập phân thứ tư), biết rằng: AB = 13, BH = 5