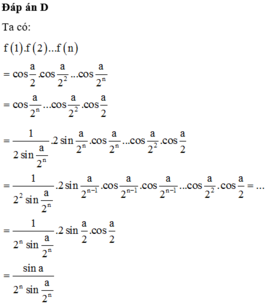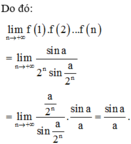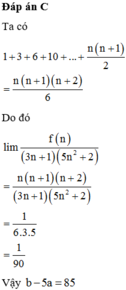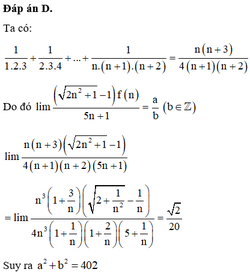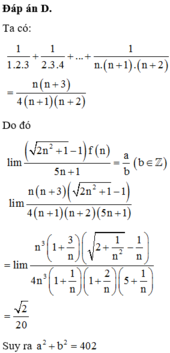Cho hàm số f n = 1 2 n - 1 , n ∈ N*. Tính f 1 , f 2 , f 3 , f 4 , f 5 .
PB
Những câu hỏi liên quan
Cho hàm số f thỏa mãn: f(1)=1; f(2)=3;f(n)+f(n+2)=2f(n+1) với mọi số nguyên dương n. Vậy f(1)+f(2)+...+f(30) bằng
cho hàm số f(x) thỏa mãn f(1)=1,f(2)=3,f(n)+f(n+2)=2*f(n+1) với mọi số nguyên dương n.tính f(1)+f(2)+...+f(2019)
cho hàm số f(x) thỏa mãn f(1)=1,f(2)=3,f(n)+f(n+2)=2*f(n+1) với mọi số nguyên dương n.tính f(1)+f(2)+...+f(2019)
Cho hàm số f(n)cos
a
2
n
,
(
a
≠
0
,
n
∈
N
)
. Tính giới hạn
lim
n
→
+
∞
(
1
)
.
f
(
2
)
.
.
.
f
(
n...
Đọc tiếp
Cho hàm số f(n)=cos a 2 n , ( a ≠ 0 , n ∈ N ) . Tính giới hạn lim n → + ∞ ( 1 ) . f ( 2 ) . . . f ( n ) .
A. sin a 2 a
B. 2 sin a a
C. sin 2 a 2 a
D. sin a a
Vẽ thuật toán và viết chương trình tính và in ra số Fibonaci F(n) với n nhập từ bàn phím. Biết F(n) = F(n-1) + F(n-2), cho trước F(1) = 1; F(2) = 1;
Gợi ý: Viết hàm số tính Fib(n) trả về giá trị số Fibonaci thứ n.
#include <bits/stdc++.h>
using namespace std;
long long n;
int main()
{
freopen("fibonacci.inp","r",stdin);
freopen("fibonacci.out","w",stdout);
cin>>n;
double c5=sqrt(5);
cout<<fixed<<setprecision(0)<<((1/c5)*(pow((1+c5)/2,n)-pow((1-c5)/2,n)));
return 0;
}
Đúng 0
Bình luận (0)
Cho hàm số
f
(
n
)
1
+
3
+
6
+
10
+
.
.
.
+
n
(
n
+
1
)
2
(
n
∈
N
*
)
. Biết lim
f
(...
Đọc tiếp
Cho hàm số f ( n ) = 1 + 3 + 6 + 10 + . . . + n ( n + 1 ) 2 ( n ∈ N * ) . Biết lim f ( n ) ( 3 n + 1 ) ( 5 n 2 + 2 ) = a b ( a , b ∈ Z ) phân số này tối giản. Giá trị b - 5a là
A. 50
B. 45
C. 85
D. 60
Cho hàm số f(n) 1+3+6+10+...+
n
(
n
+
1
)
2
(
n
∈
N
*
)
. Biết lim
f
(
n
)
(
3
n
+
1
)...
Đọc tiếp
Cho hàm số f(n)= 1+3+6+10+...+ n ( n + 1 ) 2 ( n ∈ N * ) .
Biết lim f ( n ) ( 3 n + 1 ) ( 5 n 2 + 2 ) = a b ( a , b ∈ Z ) phân số này tối giản. Giá trị b - 5a là
A.50
B.45
C.85
D.60
Cho hàm số f(n)
1
1
.
2
.
3
+
1
2
.
3
.
4
+
.
.
.
+
1
n
.
(
n
+
1
)...
Đọc tiếp
Cho hàm số f(n)= 1 1 . 2 . 3 + 1 2 . 3 . 4 + . . . + 1 n . ( n + 1 ) . ( n + 2 ) = n ( n + 3 ) 4 ( n + 1 ) ( n + 2 ) ,n∈N*. Kết quả giới hạn l i m ( 2 n 2 + 1 - 1 ) f ( n ) 5 n + 1 = a b b ∈ Z . Giá trị của a 2 + b 2 là
A. 101
B. 443
C. 363
D. 402
Cho hàm số f(n)
1
1
.
2
.
3
+
1
2
.
3
.
4
+
.
.
.
+
1
n
.
(
n
+
1
)...
Đọc tiếp
Cho hàm số f(n)= 1 1 . 2 . 3 + 1 2 . 3 . 4 + . . . + 1 n . ( n + 1 ) . ( n + 2 ) = n ( n + 3 ) 4 ( n + 1 ) ( n + 2 ) , n ∈ N * . Kết quả giới hạn lim ( 2 n 2 + 1 - 1 ) f ( n ) 5 n + 1 = a b ( b ∈ Z ) . Giá trị của a 2 + b 2 là
A.101
B.443
C.363
D.402
Cho hàm số y=f(x)+mx+n. Xác định m,n biết đồ thị hàm số đi qua M(-3 : 2 ) , N(1/2 : 5/6 )