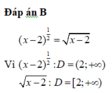Tìm tập xác định của các hàm số y = c o t 2 x
PB
Những câu hỏi liên quan
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.1. TXĐ CỦA HÀM SỐCâu 1.Tìm tập xác định của hàm số ydfrac{sqrt{x-1}}{x-3}Câu 2.Tìm tập xác định của hàm số y sqrt[3]{x-1}Câu 3. Tìm tập xác định của hàm số ydfrac{sqrt[3]{1-x}+3}{sqrt{x+3}}Câu 4. Tìm tập xác định của hàm số ysqrt{left|x-2right|}
Đọc tiếp
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.
1. TXĐ CỦA HÀM SỐ
Câu 1.Tìm tập xác định của hàm số y=\(\dfrac{\sqrt{x-1}}{x-3}\)
Câu 2.Tìm tập xác định của hàm số y= \(\sqrt[3]{x-1}\)
Câu 3. Tìm tập xác định của hàm số y=\(\dfrac{\sqrt[3]{1-x}+3}{\sqrt{x+3}}\)
Câu 4. Tìm tập xác định của hàm số y=\(\sqrt{\left|x-2\right|}\)
ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)
Đúng 1
Bình luận (0)
Tìm tập xác định của các hàm số sau:
a) \(y = 4{x^2} - 1\)
b) \(y = \dfrac{1}{{{x^2} + 1}}\)
c) \(y = 2 + \dfrac{1}{x}\)
a) Biểu thức \(4{x^2} - 1\) có nghĩa với mọi \(x \in \mathbb{R}\)
Vậy tập xác định của hàm số này là \(D = \mathbb{R}\)
b) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \({x^2} + 1 \ne 0,\)tức là với mọi \(x \in \mathbb{R}\)
Vậy tập xác định của hàm số này là \(D = \mathbb{R}\)
c) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \(\frac{1}{x}\) có nghĩa, tức là khi \(x \ne 0,\)
Vậy tập xác định của hàm số này là \(D = \mathbb{R}{\rm{\backslash }}\{ 0\} \)
Đúng 0
Bình luận (0)
Cho hàm số y=f(x) xác định bởi công thức: \(y=\frac{-18}{\left|2x-1\right|}\)
a) Tìm đk xác định và tập xác định của hàm số.
b) Biết \(x\in\left\{-4;-2;-1;0;1;2;3\right\}\). Hãy viết tập hợp các cặp số xác định bởi hàm số y=f(x)
Câu a mình làm đc r, nhờ m.n làm hộ mình câu b và ý nhỏ này nx nhé, cũng nằm trong bài.
c) Tìm \(x\in Z\) để hàm số y=f(x) đạt GTNN? Tính giá trị đó.
y= \(\dfrac{mx}{\sqrt{x-m+2}+1}\)
a, Tìm tập xác định của hàm số theo tham số m
b, Tìm m để hàm số có tập xác định trên (0;1)
Cho hàm số
y
(
x
-
2
)
-
1
2
Bạn Toán tìm tập xác định của hàm số bằng cách như sau:Bước 1: Ta có
y
1
(
x
-
2
)
1
2...
Đọc tiếp
Cho hàm số y = ( x - 2 ) - 1 2 Bạn Toán tìm tập xác định của hàm số bằng cách như sau:
Bước 1: Ta có y = 1 ( x - 2 ) 1 2 = 1 x - 2
Bước 2: Hàm số xác định ⇔ x - 2 > 0 ⇔ x > 2
Bước 3: Vậy tập xác định của hàm số là D = ( 2 ; + ∞ )
Lời giải trên của bạn toán đúng hay sai? Nếu sai thì sai ở bước nào?
A. Bước 3
B. Bước 1
C. Đúng
D. Bước 2
Tìm tập xác định của các hàm số sau:
a) \(y = \sqrt {{4^x} - {2^{x + 1}}} \)
b) \(y = \ln (1 - \ln x)\).
\(a,4^x-2^{x+1}\ge0\\ \Leftrightarrow2^{x+1}\le2^{2x}\\ \Leftrightarrow x+1\le2x\\ \Leftrightarrow x\ge1\)
Tập xác định của hàm số là D = \([1;+\infty)\)
\(b,\left\{{}\begin{matrix}x>0\\1-ln\left(x\right)>0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x>0\\ln\left(x\right)< 1\end{matrix}\right.\\ \Leftrightarrow0< x< e\)
Tập xác định của hàm số là \(\left(0;e\right)\)
Đúng 0
Bình luận (0)
Tìm tập xác định của các hàm số y = tan x + c o t x
tan x và cos x có nghĩa khi sin x ≠ 0 và cos x ≠ 0
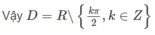
Đúng 0
Bình luận (0)
Tìm tập xác định của các hàm số sau: a) y2x^3+3x+1;b) ydfrac{x-1}{x^2-3x+2} ;��−1�2−3�+c) ysqrt{x+1}+sqrt{1-x}.
Đọc tiếp
Tìm tập xác định của các hàm số sau:
a) \(y=2x^3+3x+1\);
b) \(y=\dfrac{x-1}{x^2-3x+2}\) ;
c) \(y=\sqrt{x+1}+\sqrt{1-x}\).
a) Hàm \(y = 2{x^3} + 3x + 1\) là hàm đa thức nên có tập xác định \(D = \mathbb{R}\)
b) Biểu thức \(\frac{{x - 1}}{{{x^2} - 3x + 2}}\)có nghĩa khi \({x^2} - 3x + 2 \ne 0 \Leftrightarrow x \ne 1\)và \(x \ne 2\)
Vậy tập xác định của hàm số đã cho là \(D = \mathbb{R}/\left\{ {1;2} \right\}\)
c) Biểu thức \(\sqrt {x + 1} + \sqrt {1 - x} \) có nghĩa khi \(x + 1 \ge 0\) và \(1 - x \ge 0\), tức là \( - 1 \le x \le 1\)
Vậy tập xác định của hàm số đã cho là \(D = \left[ { - 1;1} \right]\)
Đúng 0
Bình luận (0)
Tìm tập xác định của các hàm số y = cos x + 1
Tìm tập xác định của các hàm số: y = 1 - x - 1 3
Hàm số 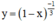 xác định
xác định
⇔ 1 – x > 0
⇔ x < 1.
Vậy tập xác định D = (-∞; 1).
Đúng 0
Bình luận (0)