Xét sự đồng biến, nghịch biến của hàm số:
y = 4 + 3x – x2
Xét sự đồng biến, nghịch biến của hàm số: y = - x 3 + x 2 - 5
Tập xác định: D = R
y'= -3x2 + 2x
y' = 0 ⇔ -3x2 + 2x = 0 ⇔ x.(-3x + 2) = 0 ⇔ 
Bảng biến thiên:
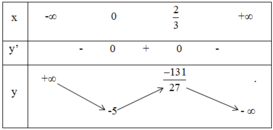
Vậy hàm số nghịch biến trong các khoảng (-∞ ; 0) và (2/3 ; + ∞), đồng biến trong khoảng (0 ; 2/3).
Xét sự đồng biến, nghịch biến của hàm số: a) y = 4 + 3x – x2 Giải bài tập Giải tích 12 | Để học tốt Toán 12 c) y = x4 - 2x2 + 3 d) y = -x3 + x2 – 5
Lớp 12 đấy!
Xét sự đồng biến, nghịch biến của các hàm số: y = x 3 − 6 x 2 + 9x
TXĐ: R
y′ = 3 x 2 − 12x + 9
y' = 0
y' > 0 trên các khoảng (- ∞ ; 1), (3; + ∞ ) nên y đồng biến trên các khoảng (- ∞ ; 1), (3; + ∞ )
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
Xét sự đồng biến, nghịch biến của các hàm số: y = x 4 + 8 x 2 + 5
TXĐ: R
y′ = 4 x 3 + 16 = 4x( x 2 + 4)
y' = 0 ⇔ 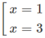
y' > 0 trên khoảng (0; + ∞ ) ⇒ y đồng biến trên khoảng (0; + ∞ )
y' < 0 trên khoảng (- ∞ ; 0) ⇒ y nghịch biến trên khoảng (- ∞ ; 0)
Xét sự đồng biến, nghịch biến của các hàm số: y = 16x + 2 x 2 − 16 x 3 /3 − x 4
TXĐ: R
y′ = 16 + 4x − 16 x 2 − 4 x 3 = −4(x + 4)( x 2 − 1)
y' = 0 ⇔ 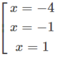
Bảng biến thiên:
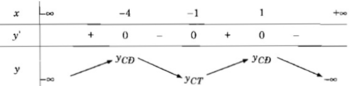
Vậy hàm số y đã cho đồng biến trên các khoảng (- ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )
Xét sự đồng biến, nghịch biến của các hàm số
a) y=4+3x−x2.
b) y=13x3+3x2−7x−2.
c) y=x4−2x2+3.
d) y=−x3+x2−5.
Giải giúp mình nhé!!!
Cho hàm số y = f(x) = -1,5 x 2
Phát biểu nhận xét của em về sự đồng biến hay nghịch biến của hàm số này khi x > 0 ; khi x < 0
Hàm số y = f(x) = -1,5 x 2 có hệ số a = -1,5 < 0 nên hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Xét sự đồng biến, nghịch biến của hàm số
a, y = \(x\sqrt{1-x^2}\)
b,y = \(\sqrt{3x^2-x^3}\)
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = 3 x 2 − 8 x 3
b) y = 16x + 2 x 2 − 16 x 3 /3 − x 4
c) y = x 3 − 6 x 2 + 9x
d) y = x 4 + 8 x 2 + 5
a) TXĐ: R
y′ = 6x − 24 x 2 = 6x(1 − 4x)
y' = 0 ⇔ 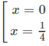
y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)
y' < 0 trên các khoảng ( - ∞ ; 0 ); (14; + ∞ ), suy ra y nghịch biến trên các khoảng ( - ∞ ;0 ); (14; + ∞ )
b) TXĐ: R
y′ = 16 + 4x − 16 x 2 − 4 x 3 = −4(x + 4)( x 2 − 1)
y' = 0 ⇔ 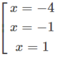
Bảng biến thiên:
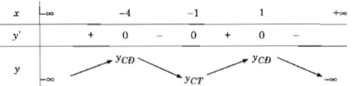
Vậy hàm số y đã cho đồng biến trên các khoảng ( - ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )
c) TXĐ: R
y′ = 3 x 2 − 12x + 9
y' = 0
y' > 0 trên các khoảng ( - ∞ ; 1), (3; + ∞ ) nên y đồng biến trên các khoảng ( - ∞ ; 1), (3; + ∞ )
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
d) TXĐ: R
y′ = 4 x 3 + 16 = 4x( x 2 + 4)
y' = 0 ⇔ 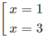
y' > 0 trên khoảng (0; + ∞ ) ⇒ y đồng biến trên khoảng (0; + ∞ )
y' < 0 trên khoảng ( - ∞ ; 0) ⇒ y nghịch biến trên khoảng ( - ∞ ; 0)