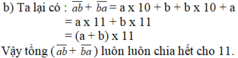cho một số có 2 chữ số có dạng ab.Chứng tỏ rằng ab+ba chia hết cho tổng (a+b)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NA
Những câu hỏi liên quan
Cho một số có hai chữ số có dạng ab .Chứng tỏ rằng ab+ba chia hết a+b
Ta co:
ab + ba = (10 . a+ b) + (10 .a + b)
= (11 . a) + (11 . b)
= 11. (a + b) chia het cho ab
Vay ab + ba chia het cho a+ b
Đúng 0
Bình luận (0)
Cho một số có 2 chữ số : a là chữ số hàng chục b là chữ số hàng đơn vị số được viết dưới dạng ab. Giả sử a > b
A) em hãy chứng tỏ rằng ( ab - ba ) luôn chia hết cho 9.
B) chứng tỏ rằng (ab + ba ) luôn luôn chia hết cho 11
Số b a là là số viết ngược của số ab
a) Ta có : ab - ba = (a0 + b) - (b0 + a)
= (10 x a + b) - (10 x b + a)
= (10 x a - a) - (10 x b - b)
= 9 x a - 9 x b
= 9 x (a - b) \(⋮\)9
=> (ab - ba) \(⋮\)9 (đpcm)
b) Ta có : ab + ba = a0 + b + b0 + a
= 10 x a + b + b x 10 + a
= (10 x a + a) + (10 x b + b)
= 11 x a + 11 x b
= 11 x (a + b) \(⋮\)11
=> (ab + ba) \(⋮\)11 (đpcm)
Đúng 0
Bình luận (0)
A ) giả sử a > b 1 đơn vị ab - ba = 9 => có thể chia hết cho 9
VD : 32 - 23 = 9 ; 9 : 9 = 1
B ) vì ab + ba = số có 2 chữ số giống nhau mà giống nhau thì luôn chia hết cho 11
VD : 21 + 12 = 33 ; 33: 11 = 3
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho 2 số có 2 chữ số: a là chữ số hàng chục và b là chữ số hàng đơn vị, sẽ được viết là ab. Giả sử aba, em hãy chứng tỏ rằng hiệu ( ab - ba ) luôn luôn chia hết cho 9.c, chứng tỏ rằng tổng ( ab + ba ) luôn luôn chia hết cho 11. Số ba la số viết ngược lại của số ab
Đọc tiếp
Cho 2 số có 2 chữ số: a là chữ số hàng chục và b là chữ số hàng đơn vị, sẽ được viết là ab. Giả sử a>b
a, em hãy chứng tỏ rằng hiệu ( ab - ba ) luôn luôn chia hết cho 9.
c, chứng tỏ rằng tổng ( ab + ba ) luôn luôn chia hết cho 11. Số ba la số viết ngược lại của số ab ![]()
Cho 1 số có 2 chữ số có dạng ab
a. Chứng minh rằng tổng ab + ba thì chia hết cho tổng a + b
b. Chứng minh rằng hiệu ab - ba thì chia hết cho hiệu a - b, với a>b
a) ab + ba
= 10a + b + 10b + a
= 11a + 11b = 11(a+b)
Chia hết cho a + b
Đúng 0
Bình luận (0)
a) ab + ba
= 10a + b + 10b + a
= 11a + 11b = 11(a+b)
Chia hết cho a + b
Đúng 0
Bình luận (0)
a)ab+ba
=10a+b+10b+a
=11a+11b=11(a+b)
chai hết cho a+b
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho 2 số có 2 chữ số: a là chữ số hàng chục và b là chữ số hàng đơn vị, sẽ được viết là ab. Giả sử a>b
a, em hãy chứng tỏ rằng hiệu ( ab - ba ) luôn luôn chia hết cho 9.
c, chứng tỏ rằng tổng ( ab + ba ) luôn luôn chia hết cho 11. Số ba la số viết ngược lại của số ab.
c, Ta có ab+ba = 10a + 10b + a + b=11a + 11b
Vậy ab+ba chia hết cho 11
Đúng 0
Bình luận (0)
Cho một số có 2 chữ số: a là chữ số hàng chục và b là chữ số hàng đơn vị, số được viết là
a
b
¯
. Giả sử a bb) Chứng tỏ rằng tổng (
a
b
¯
+
b
a
¯
) luôn luôn chia hết cho 11. Số
b
a...
Đọc tiếp
Cho một số có 2 chữ số: a là chữ số hàng chục và b là chữ số hàng đơn vị, số được viết là a b ¯ . Giả sử a > b
b) Chứng tỏ rằng tổng ( a b ¯ + b a ¯ ) luôn luôn chia hết cho 11. Số b a ¯ là số viết ngược lại của số a b ¯ .
Cho 2 số có 2 chữ số: a là chữ số hàng chục và b là chữ số hàng đơn vị, sẽ được viết là ab. Giả sử a>ba
Em hãy chứng tỏ rằng hiệu ( ab - ba ) luôn luôn chia hết cho 9.
Chứng tỏ rằng tổng ( ab ba ) luôn luôn chia hết cho 11. Số ba là số viết ngược lại của số ab.
a) Ta có : ab - ba
= ( 10 x a + b ) - ( 10 x b + a )
= ( 10 x a - a ) - ( 10 x b - b )
= 9 x a - 9 x b
= 9 x ( a - b )
\(\Rightarrow\)ab - ba chia hết cho 9
b) Ta có: ab + ba
= ( 10 x a + b ) + ( 10 x b + a )
= ( 10 x a + a ) + ( 10 x b + b )
= 11 x a + 11 x b
= 11 x ( a + b )
\(\Rightarrow\)ab + ba chia hết cho 11
Nhớ k chị nha. Chúc em học tốt.
Đúng 2
Bình luận (0)
a)Ta có:
ab-ba =a.10+b-b.10-a
=a.9-b.9
Mà a > b nên thương nhỏ nhất của hai số sẽ bằng 9.
=> ab-ba luôn chia hết cho 9
b) ab+ba =a.10+b+b.10+a
=a.11+b.11
=(a+b).11
=> ab+ba luôn chia hết cho 11
Đúng 0
Bình luận (0)
???????????????????
Cho 1 số có 2 chữ số : a là chữ số hàng chục và b là chữ số thuộc hàng đơn vị , sẽ được ab . Giả sử a > b
a) Em hãy chứng tỏ rằng hiệu ( ab - ba ) luôn luôn chia hết cho 9
Chứng tỏ rằng tổng ( ab + ba ) luôn luôn chia hết cho 11 . Số ba là số viết ngược lại của số ab
hộ mình nhé mình đang cần gấp
a) ab=a.10+b
ba=b.10+a
ab-ba=10a+b-10b-a
=9a-9.b
Giả sử a lớn hơn b n đơn vị, ta có:
(b+n)9-9b
=n.9 => ab-ba luôn chia hết cho 9
b) ab=10a+b
ba=10b+a
ab+ba=10a+a+10b+b
=11a+11b
=(a+b)11
=> ab+ba luôn chia hết cho 11
chúc bạn học tốt nha
Đúng 0
Bình luận (0)
Ta có: ab - ba = 10a + b - (10b + a) = 10a + b - 10b - a = 9a - 9b = 9 x (a - b)
Vì a > b nên a - b dương => 9 x (a - b) chia hết cho 9
ab + ba = 10a + b + 10b + a = 11a + 11b = 11 x (a + b) chia hết cho 11
Đúng 0
Bình luận (0)
a)Tổng của ba số tự nhiên liên tiếp có chia hết cho 3?
b) chứng tỏ rằng tích của hai số tự nhiên liên tiếp có chia hết cho 2
c) Chứng tỏ rằng mọi số tự nhiên có ba chữ số giống nhau đều là bội của 37.
d) chứng tỏ rằng tổng ab + ba chia hết cho 11
a, gọi 3 số tự nhiên liên tiếp đó là : a; a + 1; a + 2
tổng của chúng là :
a + a + 1 + a + 2
= (a + a + a) + (1 + 2)
= 3a + 3
= 3(a + 1) ⋮ 3 (đpcm)
b, trong 2 số tự nhiên liên tiếp chắc chắn có 1 số chia hết cho 2
=> tích của chúng chia hết chô 2 (đpcm)
c, gọi số tự nhiên có 3 chữ số giống nhau là : aaa (a là chữ số)
aaa = a.111 = a.3.37 ⋮ 37 (đpcm)
d, ab + ba
= 10a + b + 10b + a
= (10a + a) + (10b + b)
= 11a + 11b
= 11(a + b) ⋮ 11 (đpcm)
Đúng 0
Bình luận (0)
d, ab + ba
= 10a + b + 10b + a
= a ( 10 + 1) + b(10+1)
= a.11 + b.11
= ( a + b ).11 \(⋮\)11
Vậy ab + ba \(⋮\)11
Hok tốt
Đúng 0
Bình luận (0)
c,
Gọi số có 3 chữ số giống nhau là aaa ( a\(\inℕ^∗\))
Ta có:
aaa = 111.a = 3.37.a \(⋮\)37 ( đpcm )
Hok tốt
Đúng 0
Bình luận (0)
Xem thêm câu trả lời