Cho tam giác ABC vuông tại A, AB = 21cm, AC = 28cm; đường phân giác góc A cắt BC tại D, đường thắng qua D song song với AB cắt AC tại E. Tính độ dài các đoạn thẳng BD,DC và DE.
PB
Những câu hỏi liên quan
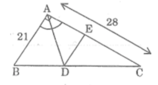
Cho tam giác ABC vuông tại A,AB=21cm,AC=28cm,đường phân giác AD.Tính khoảng cách từ D đến AC
Cho tam giác ABC vuông tại A đường cao AH biết AB= 21cm AC=28cm BC=35cm Tính AH BH CH
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=16,8\left(cm\right)\\BH=12,6\left(cm\right)\\CH=22,4\left(cm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, có AB = 21cm, AC = 28cm. Kẻ phân giác trong AD của B A C ^ (với D ∈ B C ). Tính BD, CD
Cho tam giác ABC vuông tại A, AB = 21cm, AC = 28cm; đường phân giác góc A cắt BC tại D, đường thắng qua D song song với AB cắt AC tại E. Tính diện tích tam giác ABD và diện tich tam giác ACD.
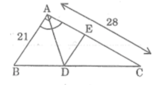
Ta có: S A B C = 1/2.AB.AC = 1/2.21.28 = 294 ( c m 2 )
Vì △ ABC và △ ADB có chung đường cao kẻ từ đỉnh A nên:
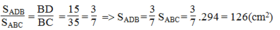
Vậy S A D C = S A B C - S A B D = 294 – 126 = 168( c m 2 )
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB=21cm, AC=28cm, đường phân giác AD.
Tính độ dài cạnh AD
Cho tam giác ABC, biết AB = 21cm, AC = 28cm, BC = 35cm. Chứng minh tam giác ABC vuông
Ta có:
A B 2 = 21 2 = 441 A C 2 = 28 2 = 784 B C 2 = 35 2 = 1225
Vì A B 2 + A C 2 = 441 + 784 = 1225 = B C 2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Đúng 0
Bình luận (0)
.cho tam giác vuông ABC ( góc A= 90 độ) AB=28cm, AC=21cm đường phân giác góc A cắt BC tại D đường thẳng qua D và song song với AC, cắt AB tại E.
a) tính BD, BC và DE
Cho ΔABC vuông tại A, đường cao AH và đường phân giác AD (H và D thuộc BC). Biết AB = 21cm, AC = 28cm.
a) Tính diện tích tam giác ABC và chứng minh AH . BC = AB . AC
\(S_{ABC}=\dfrac{AB.AC}{2}=\dfrac{21.28}{2}=294\left(cm^2\right)\)
Ta có:\(S_{ABC}=\dfrac{AB.AC}{2}\) mà ta lại có: \(S_{ABC}=\dfrac{AH.BC}{2}\)
\(\Rightarrow\dfrac{AB.AC}{2}=\dfrac{AH.BC}{2}\Rightarrow AB.AC=AH.BC\left(đpcm\right)\)
Đúng 3
Bình luận (4)
Cho tam giác ABC vuông tại A(góc A=90°),AB=21cm,AC=28cm. Vẽ đường cao AH(H thuộc BC). Tia phân giác của góc A cắt BC tại D. Tính BC,BD,CD và diện tích tam giác AHD
Xét ΔABC vuông tại A, áp dụng định lí py-ta-go ta có:
\(BC^2=AB^2+AC^2\)
\(=21^2+28^2\)
\(=1225\)
->\(BC=\sqrt{1225}=35\left(cm\right)\)
Xét ΔABC có AD là tia phân giác ta có:
\(\dfrac{AB}{BD}=\dfrac{AC}{CD}=\dfrac{AB+AC}{BC}hay\dfrac{21}{BD}=\dfrac{28}{CD}=\dfrac{21+28}{35}=\dfrac{7}{5}\)
⇒\(BD=\dfrac{21.5}{7}=15\left(cm\right)\)
⇒\(CD=\dfrac{28.5}{7}=20\left(cm\right)\)
Đúng 1
Bình luận (0)
