Cho hai đường thẳng
∆ : x - 1 2 = y + 3 1 = z - 4 - 2 ∆ ' : x + 2 - 4 = y - 1 - 2 = z + 1 4
Tính khoảng cách giữa ∆ và ∆ ′.
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
PB
Những câu hỏi liên quan
Cho hai đường thẳng y=(m 1)x-3 và y=(2m-1)x 4 a) Chứng minh rằng khi m= -1/2 thì hai đường thẳng đã cho vuông góc với nhau b) Tìm tất cả các giá trị của m để hai đường thẳng đã cho vuông góc với nhau
Ghi lại đề: \(y=\left(m+1\right)x-3;y=\left(2m-1\right)x+4\)
\(a,m=-\dfrac{1}{2}\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{2}x-3\\y=-2x+4\end{matrix}\right.\)
Hệ số a 2 đt đã cho là \(\dfrac{1}{2};-2\) có tích là -1 nên 2 đt vuông góc
\(b,\Leftrightarrow\left(m+1\right)\left(2m-1\right)=-1\\ \Leftrightarrow2m^2+m-1=-1\\ \Leftrightarrow2m^2+m=0\\ \Leftrightarrow m\left(2m-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{1}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trong không gian Oxyz , cho hai đường thẳng d1:
x
-
1
2
y
+
2
-
1
z
1
và d2:
x
1
+
4...
Đọc tiếp
Trong không gian Oxyz , cho hai đường thẳng d1: x - 1 2 = y + 2 - 1 = z 1 và d2: x = 1 + 4 t y = - 1 - 2 t z = 2 + 2 t
Khoảng cách giữa hai đường thẳng đã cho bằng
Trong không gian Oxyz, cho hai đường thẳng
d
1
:
x
-
1
+
t
y...
Đọc tiếp
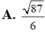
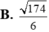
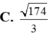
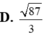
Trong không gian Oxyz, cho hai đường thẳng d 1 : x = - 1 + t y = 3 + 2 t z = - 1 - t
và d 2 : x = 7 + 3 s y = 1 - s z = 5 - s .Khoảng cách giữa hai đường thẳng đã cho bằng
A. 31
B. 6 2
C. 62
D. 4 2
cho hai đường thẳng: y = (m +1)x - 3 và y = (2m - 1)x + 4
a. chứng minh rằng khi m = -1/2 thì hai đường thẳng đã cho vuông góc với nhau
b. tìm tất cả các giá trị của m để hai đường thẳng đã cho vuông góc với nhau
Bài 1: Cho hai hàm số y(k−1)x+3�(�−1)�+3 và y(2k+1)x−4�(2�+1)�−4. Với giá trị nào của k thì đồ thị của hai hàm số là:a, Hai đường thẳng cắt nhaub, Hai đường thẳng song songc, Hai đường thẳng nói trên có thể trùng nhau được không? Vì sao?
Đọc tiếp
Bài 1: Cho hai hàm số và . Với giá trị nào của k thì đồ thị của hai hàm số là:
a, Hai đường thẳng cắt nhau
b, Hai đường thẳng song song
c, Hai đường thẳng nói trên có thể trùng nhau được không? Vì sao?
a: Để hai đường này cắt nhau thì 2k+1<>k-1
=>k<>-2
b: Để hai đường song song thì 2k+1=k-1
=>k=-2
c: Hai đường này không thể trùng nhau được bởi vì b<>b'(3<>-4)
Đúng 1
Bình luận (0)
Cho hai đường thẳng
d
1
:
x
2
+
t
y
-
1
+
t
z
3
v
à
...
Đọc tiếp
Cho hai đường thẳng d 1 : x = 2 + t y = - 1 + t z = 3 v à d 2 : x = 1 - t y = 2 z = - 2 + t . Góc giữa hai đường thẳng d1 và d2 là:
A. 30°
B. 45°
C. 90°
D. 60°
Chọn D.
Gọi u 1 → ; u 2 → lần lượt là vectơ chỉ phương của đường thẳng d1; d2.
Áp dụng công thức ta có cosin góc giữa hai đường thẳng là:
Đúng 0
Bình luận (0)
Trong không gian Oxyz cho hai đường thẳng:
d
1
:
x
1
-
t
y
t
z
-
1...
Đọc tiếp
Trong không gian Oxyz cho hai đường thẳng: d 1 : x = 1 - t y = t z = - 1 d 2 : x = 2 t ' y = - 1 + t ' z = t '
Chứng minh rằng hai đường thẳng d 1 v à d 2 chéo nhau
Cho hai đường thẳng
d
1
:
x
2
+
t
y
-
1
+
t
z
3
v
à
...
Đọc tiếp
Cho hai đường thẳng d 1 : x = 2 + t y = - 1 + t z = 3 v à d 2 : x = 1 - t y = 2 z = - 2 + t . Góc giữa hai đường thẳng d1 và d2 là:
A. 30°
B. 45°
C. 90°
D. 60°
Cho hai đường thẳng
d
1
:
x
2
+
t
y
-
1
+
t
z
3
v
à
...
Đọc tiếp
Cho hai đường thẳng d 1 : x = 2 + t y = - 1 + t z = 3 v à d 2 : x = 1 - t y = 2 z = - 2 + t . Góc giữa hai đường thẳng d1 và d2 là:
A. 30°
B. 45°
C. 90°
D. 60°
Trong không gian Oxyz, cho hai đường thẳng
d
1
:
x
-
1
2
y
+
2
-
1
z
1
và
d
2
:
x...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng d 1 : x - 1 2 = y + 2 - 1 = z 1 và d 2 : x = 1 + 4 t y = - 1 - 2 t z = 2 + 2 t , t ∈ R . Khoảng cách giữa hai đường thẳng đã cho bằng
A. 87 6
B. 174 6
C. 174 3
D. 87 3
