Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi 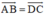
PB
Những câu hỏi liên quan
Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} \)
Tứ giác ABCD là hình bình hành
\( \Leftrightarrow \left\{ \begin{array}{l}
AB // DC\\
AB = DC
\end{array} \right.\)
Mà \(AB // DC \Leftrightarrow \overrightarrow {AB} ,\, \overrightarrow {DC} \) cùng phương, do đó cùng hướng.
\( \Leftrightarrow \left\{ \begin{array}{l}
\overrightarrow {AB} , \overrightarrow {DC} \,{\rm{ cùng hướng}}\\
AB = DC
\end{array} \right.\)
\(\Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \)
Vậy tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} \).
Đúng 1
Bình luận (0)
Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi \(\overrightarrow{AB}=\overrightarrow{DC}\) ?
Ta chứng minh hai mệnh đề:
- Khi =
thì ABCD là hình bình hành.
Thật vậy, theo định nghĩa của vec tơ bằng nhau thì:
=
⇔
=
và và
cùng hướng.
và
cùng hướng =>
và
cùng phương, suy ra giá của chúng song song với nhau, hay AB // DC (1)
Ta lại có =
=> AB = DC (2)
Từ (1) và (2), theo dấu hiệu nhận biết hình bình hành, tứ giác ABCD có một cặp cạnh song song và bằng nhau nên nó là hình bình hành.
- Khi ABCD là hình bình hành thì =
Khi ABCD là hình bình hành thì AB // CD. Dễ thấy, từ đây ta suy ra hai vec tơ và
cùng hướng (3)
Mặt khác AB = CD => =
(4)
Từ (3) và (4) suy ra =
.
Đúng 1
Bình luận (0)
Chứng minh rằng tứ giác ABCD là một hình bình hành khi và chỉ khi \(\overrightarrow {BC} = \overrightarrow {AD}.\)
Tứ giác ABCD là một hình bình hành \( \Leftrightarrow \left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\)
\( \Leftrightarrow \) Hai vecto \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) cùng hướng và AD = BC.
\( \Leftrightarrow \overrightarrow {BC} = \overrightarrow {AD} .\) (đpcm)
Đúng 0
Bình luận (0)
tứ giác ABCD có C=A và BC//AD. chứng minh rằng tứ giác đó là hình bình hành.
BC//AD nên \(\widehat{A}+\widehat{B}=180^0;\widehat{C}+\widehat{D}=180^0\)
Mà \(\widehat{A}=\widehat{C}\Rightarrow\widehat{B}=\widehat{D}\)
Vậy ABCD là hbh
Đúng 0
Bình luận (1)
Cho tứ giác ABCD có AC = BD và AC vuông góc BD. khi đó : A. Tứ giác ABCD là hình vuông B. Tứ giác ABCD là hình bình hành C. Tứ giác ABCD là hình thoi D. ABCD là tứ giác bất kì
Cho hình bình hành ABCD có AB 8 cm,AD 4 cm.Gọi M, N lần lượt là trung điểm của AB và CD.a/ Chứng minh tứ giác AMCN là hình bình hành. Hỏi tứ giác AMND là hình gì?b. Gọi I là giao điểm của AN và DM , K là giao điểm của BN và CM . Tứ giác MINK là hình gìc/ Chứng minh IKCDd/ (Lớp 8A làm thêm câu này).Hình bình hành ABCD cần thêm điều kiện gì thì tứ giác MINK là hình vuông? Khi đó ,diện tích của MINK bằng bao nhiêu?
Đọc tiếp
Cho hình bình hành ABCD có AB = 8 cm,AD = 4 cm.Gọi M, N lần lượt là trung điểm của AB và CD.a/ Chứng minh tứ giác AMCN là hình bình hành. Hỏi tứ giác AMND là hình gì?
b. Gọi I là giao điểm của AN và DM , K là giao điểm của BN và CM . Tứ giác MINK là hình gì
c/ Chứng minh IK\\CD
d/ (Lớp 8A làm thêm câu này).Hình bình hành ABCD cần thêm điều kiện gì thì tứ giác MINK là hình vuông? Khi đó ,diện tích của MINK bằng bao nhiêu?
Cho hình bình hành ABCD, Trên cạnh AB lấy điểm M, trên cạnh CD lấy điểm N sao cho a, Chứng minh rằng: . b, Chứng minh tứ giác AMCN là hình bình hành. c, Chứng minh tứ giác BMDN là hình bình hành
Đọc tiếp
Cho hình bình hành ABCD, Trên cạnh AB lấy điểm M, trên cạnh CD lấy điểm N sao cho ![]()
a, Chứng minh rằng: ![]() .
.
b, Chứng minh tứ giác AMCN là hình bình hành.
c, Chứng minh tứ giác BMDN là hình bình hành
Cho hình bình hành ABCD có AB 8 cm,AD 4 cm.Gọi M, N lần lượt là trung điểm của AB và CD.a/ Chứng minh tứ giác AMCN là hình bình hành. Hỏi tứ giác AMND là hình gì?b. Gọi I là giao điểm của AN và DM , K là giao điểm của BN và CM . Tứ giác MINK là hình gì?c/ Chứng minh IK // CDd/ Hình bình hành ABCD cần thêm điều kiện gì thì tứ giác MINK là hình vuông? Khi đó ,diện tích của MINK bằng bao nhiêu?Giúp với ạ :(
Đọc tiếp
Cho hình bình hành ABCD có AB = 8 cm,AD = 4 cm.Gọi M, N lần lượt là trung điểm của AB và CD.
a/ Chứng minh tứ giác AMCN là hình bình hành. Hỏi tứ giác AMND là hình gì?
b. Gọi I là giao điểm của AN và DM , K là giao điểm của BN và CM . Tứ giác MINK là hình gì?
c/ Chứng minh IK // CD
d/ Hình bình hành ABCD cần thêm điều kiện gì thì tứ giác MINK là hình vuông? Khi đó ,diện tích của MINK bằng bao nhiêu?
Giúp với ạ :(
Cho hình bình hành ABCD có AB=2AD.Gọi E và F lần lượt là trung điểm của AB và CD. I là giao điểm của AF và DE,K là giao điểm của BF và CE. a)Chứng minh rằng tứ giác AECF là hình bình hành. b)Tứ giác AEFD là hình gì ? Vì sao? c) Chứng minh rằng tứ giác EIFK là hình chữ nhật. d) Tìm điều kiện của hình bình hành ABCD để tứ giác EIFK là hình vuông.
a: Ta có: ABCD là hình bình hành
=>AB=CD(1)
Ta có: E là trung điểm của AB
=>\(EA=EB=\dfrac{AB}{2}\left(2\right)\)
Ta có: F là trung điểm của CD
=>\(FC=FD=\dfrac{CD}{2}\left(3\right)\)
Từ (1),(2),(3) suy ra EA=EB=FC=FD
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFDlà hình bình hành
Hình bình hành AEFD có \(AE=AD\left(=\dfrac{AB}{2}\right)\)
nên AEFD là hình thoi
c: Xét tứ giác EBCF có
BE//FC
BE=FC
Do đó: EBCF là hình bình hành
Hình bình hành EBCF có \(EB=BC\left(=\dfrac{AB}{2}\right)\)
nên EBCF là hình thoi
=>EC\(\perp\)BF tại trung điểm của mỗi đường
=>EC\(\perp\)BF tại K và K là trung điểm chung của EC và BF
Ta có: AEFD là hình thoi
=>AF\(\perp\)ED tại trung điểm của mỗi đường
=>AF\(\perp\)ED tại I và I là trung điểm chung của AF và ED
Ta có: AEFD là hình thoi
=>EF=AD
mà AD=DC/2
nên EF=DC/2
Xét ΔEDC có
EF là đường trung tuyến
\(EF=\dfrac{CD}{2}\)
Do đó: ΔEDC vuông tại E
Xét tứ giác EIFK có
\(\widehat{EIF}=\widehat{EKF}=\widehat{IEK}=90^0\)
=>EIFK là hình chữ nhật
d: Để EIFK là hình vuông thì FI=FK
mà \(FI=\dfrac{FA}{2};FK=\dfrac{FB}{2}\)
nên FA=FB
=>ΔFAB cân tại F
Ta có: ΔFAB cân tại F
mà FE là đường trung tuyến
nên FE\(\perp\)AB
ta có: FE\(\perp\)AB
FE//AD
Do đó: AD\(\perp\)AB
Đúng 2
Bình luận (0)


