Cho các bộ ba đoạn thẳng có độ dài như sau:
1cm; 2cm; 3,5cm
PB
Những câu hỏi liên quan
Cho các bộ ba đoạn thẳng có độ dài như sau:
a) 2cm; 3cm; 4cm
b) 1cm; 2cm; 3,5cm
c) 2,2cm; 2cm; 4,2cm
Hãy vẽ tam giác có độ dài ba cạnh lần lượt là một trong các bộ ba ở trên (nếu vẽ được). Trong trường hợp không vẽ được, hãy giải thích.
a) Với 3 độ dài 2cm, 3cm, 4cm lập thành 3 cạnh của Δ.
b) 1cm; 2cm; 3,5cm không lập thành 3 cạnh của Δ vì 2 – 1 < 3,5 < 2 + 1 BĐT sai
c) 2,2 + 2 = 4,2 không lập thành Δ
Đúng 0
Bình luận (0)
Cho các bộ ba đoạn thẳng có độ dài như sau:
2,2cm; 2cm; 4,2cm
2,2cm + 2cm = 4,2cm.
⇒ Bộ ba đoạn thẳng 2,2cm; 2cm; 4,2cm không lập thành tam giác.
Đúng 0
Bình luận (0)
Cho các bộ ba đoạn thẳng có độ dài như sau:
2cm; 3cm; 4cm
Ta có 2cm + 3cm = 5cm > 4cm.
Do đó bộ đoạn thẳng 2cm, 3cm, 4cm có thể thành 3 cạnh của tam giác.
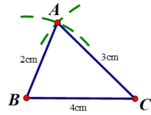
Cách dựng tam giác có ba độ dài 2cm, 3cm, 4cm
- Vẽ BC = 4cm
- Dựng đường tròn tâm B bán kính 2cm ; đường tròn tâm C bán kính 3cm. Hai đường tròn cắt nhau tại A. Nối AB, AC ta được tam giác cần dựng.
Đúng 0
Bình luận (0)
Câu 5: Trong các bộ ba đoạn thẳng có độ dài cho sau đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?A. 3cm; 3cm; 6cmB. 1cm; 2cm; 3cmC. 6cm; 8cm; 9cmD.10cm; 6cm; 7cmCâu 6: Tam giác ABC cân tại A, đường cao AH. Biết AB AC 10cm; BC 12cm. Độ dài đường cao AH là:A. 7cm B. 8cmC. 6cmD. 10cmCâu 7: Cho tam giác DEF có DE 1cm; DF 7cm. Biết độ dài cạnh EF là một số nguyên. Vậy EF có độ dài là:A. 7cmB. 6cmC. 8cmD. 9cmCâu 8: △DCE có đường cao DM và CN cắt nhau tại H. Khi đó:A. EH ⊥ CN B. EH⊥ DM...
Đọc tiếp
Câu 5: Trong các bộ ba đoạn thẳng có độ dài cho sau đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?
A. 3cm; 3cm; 6cm
B. 1cm; 2cm; 3cm
C. 6cm; 8cm; 9cm
D.10cm; 6cm; 7cm
Câu 6: Tam giác ABC cân tại A, đường cao AH. Biết AB = AC = 10cm; BC = 12cm. Độ dài đường cao AH là:
A. 7cm
B. 8cm
C. 6cm
D. 10cm
Câu 7: Cho tam giác DEF có DE = 1cm; DF = 7cm. Biết độ dài cạnh EF là một số nguyên. Vậy EF có độ dài là:
A. 7cm
B. 6cm
C. 8cm
D. 9cm
Câu 8: △DCE có đường cao DM và CN cắt nhau tại H. Khi đó:
A. EH ⊥ CN
B. EH⊥ DM
C. EH ⊥ DE
D. EH ⊥ DC
Câu 5: C,D
Câu 6; B
Câu 7: A
Câu 8:B
Đúng 1
Bình luận (0)
Bài 18 :Cho các bộ 3 đoạn thẳng có độ dài như sau :
a, 2cm ; 3cm ;4 cm
b,1cm ; 2cm ; 3,5cm
c,2,2cm ;2cm ; 4,2 cm
Hãy vẽ các tam giác có độ dài 3 cạnh lần lượt là một trong các bộ 3 ở trên ( nêú vẽ được ) . Trong trường hợp không vẽ được hãy giải thích
Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác. Trong những trường hợp còn lại, hãy thử dựng tam giác có độ dài ba cạnh như thế:
3cm, 4cm, 6cm
Ta có : 4cm + 3cm = 7cm > 6cm.
⇒ Bộ ba đoạn thẳng 3cm, 4cm, 6cm thỏa mãn bất đẳng thức tam giác nên là ba cạnh của tam giác.
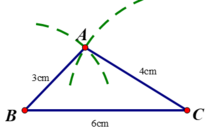
Cách dựng tam giác có ba độ dài 3cm, 4cm, 6cm
- Vẽ BC = 6cm
- Dựng đường tròn tâm B bán kính 3cm ; đường tròn tâm C bán kính 4cm. Hai đường tròn cắt nhau tại A. Nối AB, AC ta được tam giác cần dựng.
Đúng 0
Bình luận (0)
Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác. Trong những trường hợp còn lại, hãy thử dựng tam giác có độ dài ba cạnh như thế:
2cm, 4cm, 6cm
Vì 6cm = 2cm + 4cm
⇒ Bộ ba đoạn thẳng 2cm, 4cm, 6cm không thỏa mãn bất đẳng thức tam giác nên không phải là ba cạnh của tam giác.
Đúng 0
Bình luận (0)
Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác. Trong những trường hợp còn lại, hãy thử dựng tam giác có độ dài ba cạnh như thế:
2cm, 3cm, 6cm
Ta có: 3cm + 2cm = 5cm < 6cm
⇒ Bộ ba đoạn thẳng 2cm, 3cm, 6cm không thỏa mãn bất đẳng thức tam giác nên không phải là ba cạnh của tam giác.
Đúng 0
Bình luận (0)
Có thể vẽ được mấy tam giác (phân biệt) với ba cạnh là ba trong năm đoạn thẳng có độ dài như sau: 1cm, 2cm, 3cm, 4cm và 5cm?
Trong một tam giác, độ dài một cạnh lớn hơn hiệu và nhỏ hơn tổng của hai cạnh còn lại.
Vậy nên với năm đoạn thẳng có độ dài 1cm, 2cm, 3cm, 4cm, 5cm ta dựng được tam giác với ba cạnh là các đoạn thẳng có độ dài là:
+ Bộ ba 2cm, 3cm, 4cm (3-2 < 4 < 3+2)
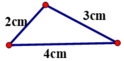
Dựng đoạn thẳng bằng 4cm.
Từ hai đầu đoạn thẳng dựng các cung tròn bán kính lần lượt 2cm và 3cm.
Hai cung tròn này cắt nhau tại điểm thứ 3.
Nối các điểm ta được tam giác cần dựng.
+ Bộ ba 3cm, 4cm, 5cm (4-3 < 5 < 4+3)
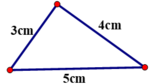
Dựng đoạn thẳng bằng 4cm.
Dựng đoạn thẳng bằng 5cm.
Từ hai đầu đoạn thẳng dựng các cung tròn bán kính lần lượt 3cm và 4cm.
Hai cung tròn này cắt nhau tại điểm thứ 3.
Nối các điểm ta được tam giác cần dựng.
+ Bộ ba 2cm, 4cm, 5cm (4-2 < 5 < 4+2)
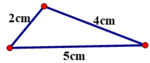
Dựng đoạn thẳng bằng 4cm.
Dựng đoạn thẳng bằng 5cm.
Từ hai đầu đoạn thẳng dựng các cung tròn bán kính lần lượt 2cm và 4cm.
Hai cung tròn này cắt nhau tại điểm thứ 3.
Nối các điểm ta được tam giác cần dựng.
Vậy ta dựng được tất cả 3 tam giác.
Đúng 0
Bình luận (0)