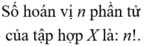Viết công thức tính số hoán vị của tập hợp gồm n phần tử n > 1 . Nêu ví dụ.
PB
Những câu hỏi liên quan
Viết công thức tính số chỉnh hợp chập k của n phần tử, công thức tính số tổ hợp chập k của n phần tử. Cho ví dụ.
+ Số chỉnh hợp chập k của n phần tử:
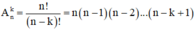
+ Số tổ hợp chập k của n phần tử:
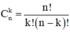
+ Ví dụ:
- Số chỉnh hợp chập 3 của 5: 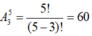
- Số tổ hợp chập 3 của 5: 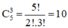
- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau để cắm vào 5 lọ khác nhau:
⇒ Có 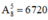 cách chọn.
cách chọn.
- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau
⇒ Có 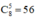 cách chọn.
cách chọn.
Đúng 0
Bình luận (0)
Cho tập hợp X có n phần tử n ∈ N * , số hoán vị n phần tử của tập hợp X là
A.n!
B.n
C. n 2
D. n 3
Cho tập hợp X có n phần tử
n
∈
N
*
, số hoán vị n phần tử của tập hợp X là A. n! B. n C.
n
2
D.
n
3
Đọc tiếp
Cho tập hợp X có n phần tử n ∈ N * , số hoán vị n phần tử của tập hợp X là
A. n!
B. n
C. n 2
D. n 3
Cho tập hợp X gồm 10 phần tử. Số các hoán vị của 10 phần tử của tập hợp X là A.
10
!
B.
10
2
C.
2
10
D.
10
10
Đọc tiếp
Cho tập hợp X gồm 10 phần tử. Số các hoán vị của 10 phần tử của tập hợp X là
A. 10 !
B. 10 2
C. 2 10
D. 10 10
Đáp án A
Phương pháp giải: Hoán vị của n phần tử chính là n giai thừa
Lời giải: Số các hoán vị của 10 phần tử của tập hợp X là 10!
Đúng 0
Bình luận (0)
Cho tập hợp X gồm 10 phần tử. Số các hoán vị của 10 phần tử của tập hợp X là
A. 10!.
B. 102.
C. 210.
D. 1010.
Đáp án A.
Phương pháp giải: Hoán vị của n phần tử chính là n giai thừa
Lời giải: Số các hoán vị của 10 phần tử của tập hợp X là 10!.
Đúng 0
Bình luận (0)
Có bao nhiêu cách xếp số 7 và 8 vào tập hợp gồm n phần tử?
Ví dụ: n = 2
[7,7], [7,8], [8,7], [8,8]
Có 2 cách xếp số 7 và 8 vào tập hợp gồm n = 2 phần tử.
Đó là: {7; 8} ; {8; 7}
Đúng 0
Bình luận (0)
1. Cho tập Xleft{1,2,...,nright}, ở đó ninℕ^∗. Chứng minh rằng số các tổ hợp gồm r phần tử của X không chứa bất kì 2 phần tử liên tiếp nào là C^r_{n-r+1} với 0le rle n-r+1
2. Một hoán vị x_1,x_2,...,x_{2n} của tập left{1,2,...,2nright} (với ninℕ) được gọi là có tính chất T nếu left|x_i-x_{i+1}right|n với ít nhất một chỉ số i thuộc tập left{1,2,...,2n-1right}. Chứng minh rằng với mọi n , có nhiều hoán vị có tính chất T hơn là những hoán vị không có tính chất T.
Giúp mình làm những bài này vớ...
Đọc tiếp
1. Cho tập \(X=\left\{1,2,...,n\right\}\), ở đó \(n\inℕ^∗\). Chứng minh rằng số các tổ hợp gồm \(r\) phần tử của \(X\) không chứa bất kì 2 phần tử liên tiếp nào là \(C^r_{n-r+1}\) với \(0\le r\le n-r+1\)
2. Một hoán vị \(x_1,x_2,...,x_{2n}\) của tập \(\left\{1,2,...,2n\right\}\) (với \(n\inℕ\)) được gọi là có tính chất \(T\) nếu \(\left|x_i-x_{i+1}\right|=n\) với ít nhất một chỉ số \(i\) thuộc tập \(\left\{1,2,...,2n-1\right\}\). Chứng minh rằng với mọi \(n\) , có nhiều hoán vị có tính chất \(T\) hơn là những hoán vị không có tính chất \(T\).
Giúp mình làm những bài này với. Mình nghĩ mãi vẫn không nghĩ ra lời giải nào thỏa đáng. Mình cảm ơn trước.
Số hoán vị của một tập hợp gồm 10 phần tử bằng
A. 2 10
B. 10!
C. 10 10
D. 10 2
Viết công thức tính công cơ học trong trường hợp hướng của lực tác dụng trùng với hướng dịch chuyển của điểm đặt lực. Nêu tên đơn vị đo công. Nêu được ví dụ trong đó lực thực hiện công hay không thực hiện công.