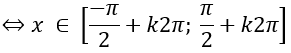Nêu định nghĩa các hàm số lượng giác. Chỉ rõ tập xác định và tập giá trị của từng hàm số đó.
PB
Những câu hỏi liên quan
Hãy cho một ví dụ về hàm số được cho bằng bảng hoặc biểu đồ. Hãy chỉ ra tập xác định và tập giá trị của hàm số đó.
Ví dụ hàm số $y=\frac{-1}{2}x$
Ta có bảng sau:

Với mỗi giá trị của x ta có 1 giá trị của y, vậy bảng trên biểu thị cho 1 hàm số
Tập xác định của hàm số \(D = \left\{ { - 2; - 1; - \frac{1}{2};0;\frac{1}{2};1;2} \right\}\)
Tập giá trị của hàm số \(\left\{ {1;\frac{1}{2};\frac{1}{4};0; - \frac{1}{4}; - \frac{1}{2}; - 1} \right\}\)
Đúng 0
Bình luận (0)
Tìm tập xác định và tập giá trị của các hàm số sau:
Cho hàm số
y
-
m
x
+
3
3
x
-
m
với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên từng khoảng xác định của nó. Tìm số phần tử của tập S
Đọc tiếp
Cho hàm số y = - m x + 3 3 x - m với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên từng khoảng xác định của nó. Tìm số phần tử của tập S
![]()
![]()
![]()
![]()
Cho hàm số
y
-
mx
+
3
3
x
-
m
với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên từng khoảng xác định của nó. Tìm số phần tử của tập S A. 5. B. 4. C. 6. D. 8.
Đọc tiếp
Cho hàm số y = - mx + 3 3 x - m với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên từng khoảng xác định của nó. Tìm số phần tử của tập S
A. 5.
B. 4.
C. 6.
D. 8.
Tìm các giá trị thực của tham số m để đồ thị hàm số
y
m
x
+
2
2
x
+
m
đồng biến trên từng khoảng thuộc tập xác định. A.
m
≥
2
. B.
m
2
. C.
∀
m
∈...
Đọc tiếp
Tìm các giá trị thực của tham số m để đồ thị hàm số y = m x + 2 2 x + m đồng biến trên từng khoảng thuộc tập xác định.
A. m ≥ 2 .
B. m > 2 .
C. ∀ m ∈ ℝ .
D. m < 2 .
Đáp án B
Điều kiện: x ≠ − m 2 .
y ' = m 2 − 4 2 x + m 2 ;
Hàm số đồng biến trên từng khoảng thuộc tập xác định
⇔ y ' > 0, ∀ x ≠ − m 2 ⇔ m 2 − 4 > 0, ∀ x ≠ − m 2 ⇔ m > 2.
Đúng 0
Bình luận (0)
Cho hàm số y=2x. Khẳng định nào sau đây là sai?
A. Tập xác định của hàm số là R.
B. Tập giá trị của hàm số là (0;+∞).
C. Đồ thị của hàm số cắt trục Ox tại đúng một điểm.
D. Hàm số đồng biến trên tập xác định của nó.
Đồ thị này cắt trục Ox tại rất nhiều điểm chứ không phải chỉ có 1 điểm
=>Chọn C
Đúng 0
Bình luận (0)
Hàm số nào sau đây có đạo hàm luôn âm với mọi giá trị thuộc tập xác định của hàm số đó? A.
y
x
3
+
x
B.
y
x
5
+
2
x
C.
y
2
-
x
3
-
x...
Đọc tiếp
Hàm số nào sau đây có đạo hàm luôn âm với mọi giá trị thuộc tập xác định của hàm số đó?
A. y = x 3 + x
B. y = x 5 + 2 x
C. y = 2 - x 3 - x
D. y = x 2 + x
Cho hàm số
y
m
x
+
2016
m
+
2017
−
x
−
m
với m là tham số thực. Gọi S là tập hợp các giá trị nguyên của m để hàm số đồng biến trên từng khoảng xác định. Tính số phần tử của S. A.2017 B.2018 C.2016 D.2019
Đọc tiếp
Cho hàm số y = m x + 2016 m + 2017 − x − m với m là tham số thực. Gọi S là tập hợp các giá trị nguyên của m để hàm số đồng biến trên từng khoảng xác định. Tính số phần tử của S.
A.2017
B.2018
C.2016
D.2019
Đáp án C
Ta có y ' = − m 2 + 2016 m + 2017 x + m 2 , y ' = 0 đồng biến trên từng khoảng xác định nếu
y ' > 0 ∀ x ∈ D ⇔ − m 2 + 2016 m + 2017 > 0 ⇔ m ∈ − 1 ; 2017
Ta đếm số nguyên trong
− 1 ; 2017 thì có 2016 số nguyên trong đó.
Đúng 0
Bình luận (0)
Cho hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) có \(f(0) = 1,f(1) = 2,f(2) = 5.\)
a) Hãy xác định giá trị của các hệ số \(a,b\) và \(c.\)
b) Xác định tập giá trị và khoảng biến thiên của hàm số.
Tham khảo:
a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\)
Lại có:
\(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\)
\(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\))
Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\)
b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \)
Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\)
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\)
Hay \(S\left( {0;1} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:

Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
Đúng 0
Bình luận (0)