Viết toạ độ các điểm A, B, C, D, E, F, G. trong hình dưới:
PB
Những câu hỏi liên quan
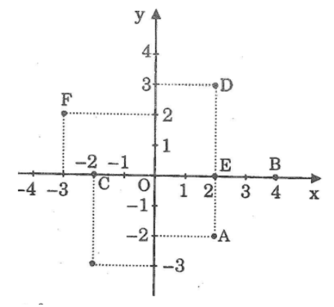
Viết tọa độ điểm A, B, C, D, E, F, G trong hình 32.
Tọa độ các điểm đó là:
A(-2; 2) ; B(-4; 0)
C(1; 0) ; D(2; 4)
E(3; -2) ; F(0; -2)
G(-3; -2)
Đúng 0
Bình luận (0)
Cho tam giác ABC có A(1; 2), B(–2; 6), C(9; 8).a Tính . Cm tam giác ABC vuông tại A.b Tìm tâm và bán kính đường tròn ngoại tiếp tam giác ABC.c Tìm toạ độ trực tâm H và trọng tâm G của tam giác ABC.d Tính chu vi, diện tích tam giác ABC.e Tìm toạ độ điểm M trên Oy để B, M, A thẳng hàng.f Tìm toạ độ điểm N trên Ox để tam giác ANC cân tại N.g Tìm toạ độ điểm D để ABDC là hình chữ nhật.h Tìm toạ độ điểm K trên Ox để AOKB là hình thang đáy AO.
Đọc tiếp
Cho tam giác ABC có A(1; 2), B(–2; 6), C(9; 8).
a Tính . Cm tam giác ABC vuông tại A.
b Tìm tâm và bán kính đường tròn ngoại tiếp tam giác ABC.
c Tìm toạ độ trực tâm H và trọng tâm G của tam giác ABC.
d Tính chu vi, diện tích tam giác ABC.
e Tìm toạ độ điểm M trên Oy để B, M, A thẳng hàng.
f Tìm toạ độ điểm N trên Ox để tam giác ANC cân tại N.
g Tìm toạ độ điểm D để ABDC là hình chữ nhật.
h Tìm toạ độ điểm K trên Ox để AOKB là hình thang đáy AO.
Thành phần nào nói bậy thế. Lớp 12 mà nói thế trước mặt cô là vào Sổ Đầu Bài và viết Bản Kiểm Điểm đấy...
Xem thêm câu trả lời
Viết toạ độ các điểm M, N , P , Q trong hình dưới
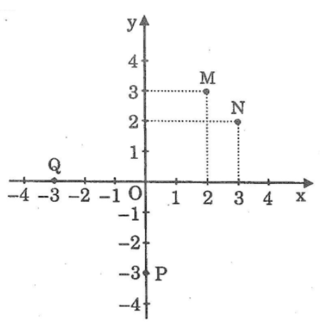
Ta có:
M(2;3), N(3;2), P(0;-3), Q(-3;0)
Đúng 0
Bình luận (0)
a) Viết tọa độ các điểm A, B, C, D, E, F, G trong hình dưới. (trong sách BT toán lp 7 tập 1 có nha)
b) Trong mặt phẳng tọa độ vẽ tam giác ABC với các đỉnh A(-3;4), B(-3;1), C(1;-1).
Trong mặt phẳng Oxy, cho hình vuông ABCD có tâm I. Biết E(2;3), F(-2;1) lần luợt là trung điểm của BC, ID và điểm A có tung độ dương. Tìm toạ độ trọng tâm G của tam giác ABC
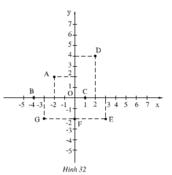
Viết tọa độ các điểm A, B, C, D, E, F trong hình 32 ?
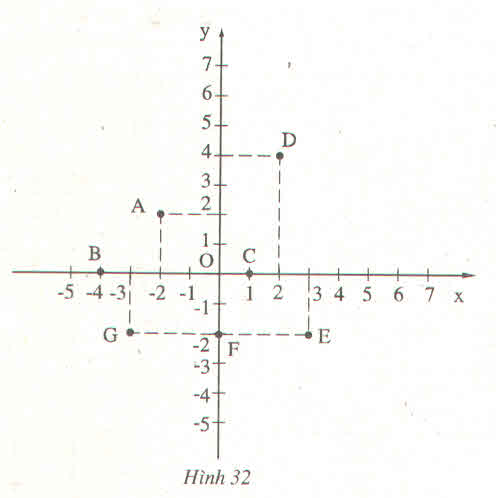
Ta có tọa độ các điểm: A(-2; 2); B(-4; 0); C(1; 0); D(2; 4); E(3; -2); F(0; -2); G(-3; -2)
Đúng 0
Bình luận (0)
Tọa độ các điểm đó là:
A(-2; 2) ; B(-4; 0)
C(1; 0) ; D(2; 4)
E(3; -2) ; F(0; -2)
G(-3; -2)
Đúng 0
Bình luận (0)
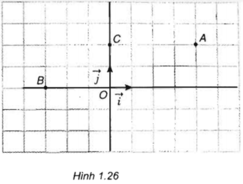
Câu hỏi 3 trang 24: Tìm tọa độ của các điểm A, B, C trong hình 1.26. Cho ba điểm D(-2; 3), E(0; -4), F(3; 0). Hãy vẽ các điểm D, E, F trên mặt phẳng Oxy.
H24
30 tháng 1 2024 lúc 19:18
Trong mặt phẳng toạ độ Oxy, cho tam giác DEF có E(-1; 0), F(3; 0). Gọi H, K lần lượt là trung điểm các cạnh DE, DF. Tìm toạ độ đỉnh D biết rằng D có toạ độ nguyên (hoành độ và tung độ là số nguyên), đồng thời hai đường trung tuyến EK, FH vuông góc với nhau.
Trong mặt phẳng toạ độ Oxy cho tam giác ABC có A(1;1) , B(2;-1) , C(3;3) . Toạ độ điểm E để tứ giác ABCE là hình bình hành là
Gọi E(x;y) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(1;-2\right)\\\overrightarrow{EC}=\left(3-x;3-y\right)\end{matrix}\right.\)
Tứ giác ABCE là hbh khi \(\overrightarrow{AB}=\overrightarrow{EC}\)
\(\Leftrightarrow\left\{{}\begin{matrix}3-x=1\\3-y=-2\end{matrix}\right.\) \(\Rightarrow E\left(2;5\right)\)
Đúng 1
Bình luận (0)