Theo như hình vẽ thì I là tâm đường tròn ngoại tiếp ABC và J là giao điểm MI với AO đúng không nhỉ?

Tam giác AMJ vuông tại J nên theo Pitago: \(MJ^2=MA^2-AJ^2\)

Tương tự tam giác vuông MJO: \(MJ^2=MO^2-JO^2\)

Trừ vế theo vế: \(MA^2-AJ^2-MO^2+JO^2=0\) (1)

Tam giác vuông AIJ: \(IJ^2=AI^2-AJ^2\)

Tam giác vuông \(IJO\): \(IJ^2=OI^2-JO^2\)

\(\Rightarrow AI^2-AJ^2-OI^2+JO^2=0\) (2)

Trừ vế (1) và (2): \(MA^2-AI^2-MO^2+OI^2=0\) (3)

Do O là trung điểm BC nên \(IO\perp BC\)

\(\Rightarrow OI^2+OC^2=IC^2\) 

Do M, C cùng thuộc đường tròn tâm O đường kính BC \(\Rightarrow OC=OM\)

Do I là tâm đường tròn ngoại tiếp ABC \(\Rightarrow IC=IA\)

\(\Rightarrow OI^2+OM^2=IA^2\Rightarrow OI^2-IA^2=-OM^2\)

Thế vào (3):

\(MA^2-MO^2-MO^2=0\Rightarrow MA=MO\sqrt{2}=\dfrac{BC\sqrt{2}}{2}\Rightarrow BC=\sqrt{2}MA\)

Em vẽ hình ra được không nhỉ? Hiện tại đang không có công cụ vẽ hình nên không hình dung được dạng câu c

câu C.

Do Tâm đường tròn ngoại tiếp tam giác thuộc đường thẳng đó nên gọi tâm đó là I 

=> I là giao điểm của đường thẳng qua M vuông góc AO, và trung trực của BC

Gọi điểm N là giao điểm cả AO và BM

=> tam giác AMO vuông tại M, MN vuông góc AO => \(AM^2\) = AN.AO

AK cắt BM tại G => AN.AO = AG.AK

Chứng minh tứ giác nội tiếp và tam giác đồng dạng  => AG.AK = 2.BN.BI = 2\(BO^2\)

=> \(AM^2=2BO^2=2BC\)

⇒ BC=\(\sqrt{2}\) AM(đpcm) 

Nhiều như vậy vừa nhìn đã choáng rồi làm gì còn đầu óc đâu mà giải nữa.

mk đâu có bắt bn giải hết đâu

ko bt hỏi ng khác ik ha

Bấm máy tính cho lẹ em ơi :))

Thực ra thì em vẫn nên sử dụng máy tính là tốt nhất vì với môn hóa thì quá trình giải hệ phương trình không quan trọng. Hơn nữa lên lớp 9 em cũng sẽ được học chi tiết cách giải hệ phương trình trong môn toán nhé!

\(\left\{{}\begin{matrix}24x+27y=6,45\\x+\dfrac{3}{2}y=0,325\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}24x+27y=6,45\\x=0,325-\dfrac{3}{2}y\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}24\left(0,325-\dfrac{3}{2}y\right)+27y=6,45\\x=0,325-\dfrac{3}{2}y\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}7,8-36y+27y=6,45\\x=0,325-\dfrac{3}{2}y\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=0,15\left(mol\right)\\x=0,325-\dfrac{3}{2}.0,15=0,1\left(mol\right)\end{matrix}\right.\)

\(3,Đk:x\ge0\\ PT\Leftrightarrow\left(\sqrt{x}-2\right)\left(2\sqrt{x}-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=2\\\sqrt{x}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=\dfrac{1}{4}\left(tm\right)\end{matrix}\right.\\ 7,ĐK:x\ge0\\ PT\Leftrightarrow\left(\sqrt{x+1}-\sqrt{x\left(x+1\right)}\right)+\left(\sqrt{x}-1\right)=0\\ \Leftrightarrow-\sqrt{x+1}\left(\sqrt{x}-1\right)+\left(\sqrt{x}-1\right)=0\\ \Leftrightarrow\left(\sqrt{x}-1\right)\left(1-\sqrt{x+1}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x+1=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=0\end{matrix}\right.\)

\(4,ĐK:1\le x\le\sqrt{5}\\ PT\Leftrightarrow5-x^2=x^2-2x+1\\ \Leftrightarrow x=-2\left(ktm\right)\Leftrightarrow x\in\varnothing\)

Tham khảo link :       https://hoc24.vn/cau-hoi/bai-6-tim-n-thuoc-z-de-phan-so-a-dfrac20n-134n-3a-a-co-gia-tri-nho-nhat-b-a-co-gia-tri-nguyen.160524630905

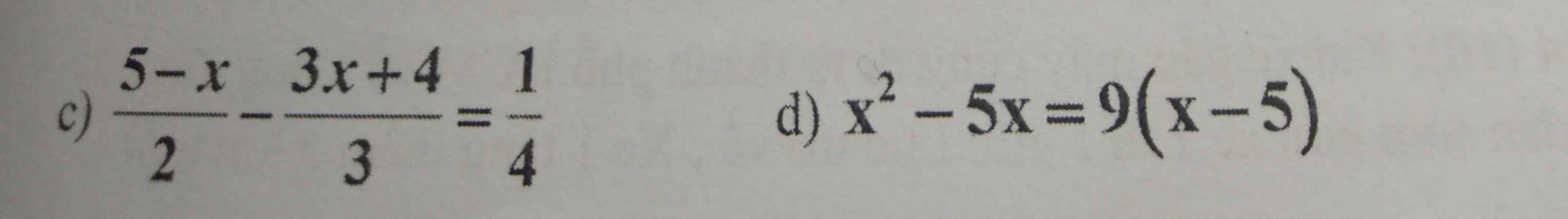
c,\(\dfrac{5-x}{2}-\dfrac{3x+4}{3}=\dfrac{1}{4}\)

⇔\(\dfrac{5-x}{2}+\dfrac{-3x-4}{3}=\dfrac{1}{4}\)

⇔\(\dfrac{6\left(5-x\right)}{12}+\dfrac{4\left(-3x-4\right)}{12}=\dfrac{3}{12}\)

⇔6(5-x)+4(-3x-4)=3

⇔   30-6x-12x-16=3

⇔            30-16-3=12x+6x

⇔                     11=18x

⇔                       x=\(\dfrac{11}{18}\)

Vậy S=\(\left\{\dfrac{11}{18}\right\}\)

d)x²-5x=9(x-5)

⇔x(x-5)=9(x-5)

⇔x(x-5)-9(x-5)=0

⇔(x-9)(x-5)=0

⇔\(\left\{{}\begin{matrix}x-9=0\Leftrightarrow x=9\\x-5=0\Leftrightarrow x=5\end{matrix}\right.\)

Vậy S=\(\left\{5;9\right\}\)

Bài 6: 

PTHH: \(Fe+2HCl\rightarrow FeCl_2+H_2\uparrow\)

              a_____2a______a_____a      (mol)

            \(2Al+6HCl\rightarrow2AlCl_3+3H_2\uparrow\)

               b______3b______b_____\(\dfrac{3}{2}\)b    (mol)

Ta lập được HPT: \(\left\{{}\begin{matrix}56a+27b=22,2\\a+\dfrac{3}{2}b=\dfrac{13,44}{22,4}=0,6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=0,3\\b=0,2\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\%m_{Fe}=\dfrac{0,3\cdot56}{22,2}\cdot100\%\approx75,68\%\\\%m_{Al}=24,32\%\end{matrix}\right.\)

\(không\) \(dùng\) \(bđt\) \(làm\) \(sao\) \(ra\) \(được\) ??

\(\sqrt{a^2+\dfrac{1}{b^2}}=\dfrac{1}{\sqrt{17}}.\sqrt{\left(1+4^2\right)\left(a^2+\dfrac{1}{b^2}\right)}\ge\dfrac{1}{\sqrt{17}}\left(a+\dfrac{4}{b}\right)\left(bunhiacopki\right)\)

\(tương-tự:\sqrt{b^2+\dfrac{1}{c^2}}\ge\dfrac{1}{\sqrt{17}}\left(b+\dfrac{4}{c}\right)\)

\(\sqrt{c^2+\dfrac{1}{a^2}}\ge\dfrac{1}{\sqrt{17}}\left(c+\dfrac{4}{a}\right)\)

\(\Rightarrow Q\ge\dfrac{1}{\sqrt{17}}\left(a+b+c+\dfrac{4}{a}+\dfrac{4}{b}+\dfrac{4}{c}\right)=\dfrac{1}{\sqrt{17}}\left[16a+\dfrac{4}{a}+16b+\dfrac{4}{b}+16c+\dfrac{4}{c}-15\left(a+b+c\right)\right]\)

\(bđt:cosi\Rightarrow16a+\dfrac{4}{a}\ge2\sqrt{16a.\dfrac{4}{a}}=2\sqrt{16.4}=16\)

\(tương-tự\Rightarrow16b+\dfrac{4}{b}\ge16;16c+\dfrac{4}{c}\ge16\)

\(có:a+b+c\le\dfrac{3}{2}\Rightarrow15\left(a+b+c\right)\le\dfrac{45}{2}\)

\(\Rightarrow-15\left(a+b+c\right)\ge-\dfrac{45}{2}\)

\(\Rightarrow Q\ge\dfrac{1}{\sqrt{17}}\left(16+16+16-\dfrac{45}{2}\right)=\dfrac{3\sqrt{17}}{2}\)

\(dấu"="xayra\Leftrightarrow a=b=c=\dfrac{1}{2}\)

các bước ban đầu dùng bunhia chọn được 1+4^2 là do dự đoán được trước điểm rơi tại a=b=c=1/2 thôi bạn,cả bước tách dùng cosi cũng dự đoán dc điểm rơi =1/2 nên tách đc thôi

Tại sao lại k được dùng nhỉ? Trông khi dùng thì bài toán sẽ dễ giải quyết hơn

Áp dụng Bunhiacopxki:

     \(\sqrt{\left(a^2+\dfrac{1}{b^2}\right)\left(\dfrac{1}{4}+4\right)}\ge\dfrac{a}{2}+\dfrac{2}{b}\)

     \(\Rightarrow\sqrt{a^2+\dfrac{1}{b^2}}\ge\dfrac{2}{\sqrt{17}}\left(\dfrac{a}{2}+\dfrac{2}{b}\right)\)

Do đó:

     \(Q\ge\dfrac{2}{\sqrt{17}}\left[\dfrac{a+b+c}{2}+2\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\right]\)

Ta có:  \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{9}{a+b+c}\)

     \(\Rightarrow Q\ge\dfrac{2}{\sqrt{17}}\left[\dfrac{a+b+c}{2}+\dfrac{18}{a+b+c}\right]\)

 Áp dụng Cô-si:

      \(\dfrac{a+b+c}{2}+\dfrac{9}{8\left(a+b+c\right)}\ge\dfrac{3}{2}\)

Do đó:

     \(Q\ge\dfrac{2}{\sqrt{17}}\left[\dfrac{3}{2}+\dfrac{135}{8\left(a+b+c\right)}\right]\ge\dfrac{2}{\sqrt{17}}\left[\dfrac{3}{2}+\dfrac{135}{8.\dfrac{3}{2}}\right]=\dfrac{3\sqrt{17}}{2}\)

Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{2}\)

Cách này 100% dùng Cô-si

Áp dụng Cô-si:

     \(Q\ge3\sqrt[3]{\sqrt{\left(a^2+\dfrac{1}{b^2}\right)\left(b^2+\dfrac{1}{c^2}\right)\left(c^2+\dfrac{1}{a^2}\right)}}\)

Ta có:

     \(A=\left(a^2+\dfrac{1}{b^2}\right)\left(b^2+\dfrac{1}{c^2}\right)\left(c^2+\dfrac{1}{a^2}\right)\)

         \(=\left(a^2+b^2+c^2\right)+\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)+\left(abc\right)^2+\dfrac{1}{\left(abc\right)^2}\)

Áp dụng Cô-si:

     \(a^2+\dfrac{1}{16a^2}\ge\dfrac{1}{2}\)

     Tương tự với các phần còn lại

\(\Rightarrow A\ge\dfrac{3}{2}+\dfrac{15}{16}\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)+\left(abc\right)^2+\dfrac{1}{\left(abc\right)^2}\)

Ta có:

     \(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\ge3\sqrt[3]{\dfrac{1}{\left(abc\right)^2}}\ge3\sqrt[3]{\dfrac{1}{\left[\dfrac{\left(a+b+c\right)^3}{27}\right]^2}}\ge12\) (Cô-si)

     \(\left(abc\right)^2+\dfrac{1}{64^2\left(abc\right)^2}\ge\dfrac{1}{32}\) (Cô-si)

\(\Rightarrow A\ge\dfrac{3}{2}+\dfrac{15}{16}.12+\dfrac{1}{32}+\dfrac{4095}{64^2\left(abc\right)^2}\)

Mà:

     \(abc\le\dfrac{\left(a+b+c\right)^3}{27}=\dfrac{1}{8}\)

\(\Rightarrow A\ge\dfrac{3}{2}+\dfrac{15}{16}.12+\dfrac{1}{32}+\dfrac{4095}{64^2.\dfrac{1}{8^2}}=\dfrac{4913}{64}\)

\(\Rightarrow Q\ge3\sqrt[3]{\sqrt{A}}\ge\dfrac{3\sqrt{17}}{2}\)