Tính tổng của S n = - ( 2 + 1 2 ) 2 + ( 4 + 1 4 ) 2 - ( 8 + 1 8 ) 2 + . . . . + ( - 1 ) n ( 2 n + 1 2 n ) 2

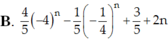


Câu 2: Viết chương trình tính tổng các chữ số của 1 số nguyên n. Kiểm tra xem tổng các số đó có là bội của 3 không?
#include <bits/stdc++.h>
using namespace std;
long long n,t,x;
int main()
{
cin>>n;
t=0;
while (n>0)
{
x=n%10;
t=t+x;
n=n/10;
}
if (t%3==0) cout<<"Co";
else cout<<"Khong";
return 0;
}
AI BIẾT LÀM BÀI NÀY CHỈ GIÚP EM VỚI Ạ!! EM CẢM ƠN
Cho tổng A = 1 + 3 + 5 +.....+(2n + 1), tổng B = 2 + 4 + 6 + 8 +.....+ 2n (n thuộc N).
a)Tính số hạng của tổng A, số hạng của tổng B
b)Chứng tỏ rằng: với mọi số tự nhiên n thì tổng A là số chính phương.
c)Tổng B có thể là số chính phương không?
\(a)\) Công thức tính số hạng của một dãy số là : (Số cuối-số đầu ) chia khoảng cách rồi cộng thêm 1 .
Do đó : Số hạng của dãy số A là : \(\dfrac{\left(2n+1\right)-1}{2}+1=n+1\)
Số hạng của dãy số B là : \(\dfrac{2n-2}{2}+1=n-1+1=n\)
\(b)\) Ta có : Số hạng của dãy số A là : \(n+1\)
Do đó : tổng của A là : \(\dfrac{\left(2n+1+1\right).\left(n+1\right)}{2}=\dfrac{2\left(n+1\right)\left(n+1\right)}{2}\)
\(=\left(n+1\right)^2\)
Vì n thuộc N nên tổng của A là : một số chính phương .
\(c)\) Ta có : Số hạng của dãy số B là : n
Do đó : Tổng của dãy số B là : \(\dfrac{n.\left(2n+2\right)}{2}=\dfrac{2.n.\left(n+1\right)}{2}\)
\(=n.\left(n+1\right)\)
Ta thấy : n(n+1) là tích của 2 số tự nhiên liên tiếp nên để B là số chính phương thì khi và chỉ khi n hoặc n+1 bằng 0 .
Ta thấy chúng đều không thoả mãn .
vậy.............
Bạn xem lại câu A+B mới là số chính phương k?
Câu a) mình không hiểu đề bài cho lắm nên mình làm câu b) với c) nhé:
Ta sẽ chứng minh \(A=1+3+5+...+\left(2n-1\right)=n^2\) bằng quy nạp. Với \(n=1\) thì \(1=1^2\), luôn đúng. Giả sử khẳng định đúng đến \(n=k\). Với \(n=k+1\) thì ta có:
\(A=1+3+5+...+\left(2k+1\right)\)
\(A=1+3+5+...+\left(2k-1\right)+\left(2k+1\right)\)
\(A=k^2+2k+1\)
\(A=\left(k+1\right)^2\) là SCP.
Vậy khẳng định được chứng minh. \(\Rightarrow\) A là SCP với mọi n (đpcm).
c) Ta có \(B=2+4+6+...+2n\)
\(B=2\left(1+2+3+...+n\right)\)
Ta sẽ chứng minh \(1+2+3+...+n=\dfrac{n\left(n+1\right)}{2}\) nhưng không phải bằng quy nạp vì mình nghĩ bạn nên biết nhiều cách khác nhau để chứng minh một đẳng thức. Mình sẽ dùng phương pháp đếm bằng 2 cách để chứng minh điều này.
Ta xét 1 nhóm gồm \(n+1\) người, mỗi người đều bắt tay đúng 1 lần với 1 người khác. Khi đó ta sẽ tính số cái bắt tay đã xảy ra bằng 2 cách:
Cách 1: Ta chọn ra 1 người, gọi là người số 1, bắt tay với \(n\) người khác. Sau đó ta chọn ra người số 2, bắt tay với \(n-1\) người khác (không tính người số 1). Chọn ra người số 3, bắt tay với \(n-2\) người (không tính người số 1 và 2). Cứ tiếp tục như thế, cho đến người thứ \(n-1\) thì sẽ có 1 cái bắt tay với người thứ \(n\). Do đó số cái bắt tay đã xảy ra là \(1+2+...+n\)
Cách 2: Số cái bắt tay chính là số cách chọn 2 người (không kể thứ tự) trong n người đó. Số cách chọn ra người thứ nhất là \(n+1\), chọn ra người thứ hai là \(n\). Do đó số cách chọn 2 người có kể thứ tự sẽ là \(n\left(n+1\right)\). Nhưng do ta không tính thứ tự nên số cái bắt tay đã xảy ra là \(\dfrac{n\left(n+1\right)}{2}\).
Do vậy, ta có \(1+2+...+n=\dfrac{n\left(n+1\right)}{2}\)
Như thế, \(B=2\left(1+2+...+n\right)=2.\dfrac{n\left(n+1\right)}{2}=n\left(n+1\right)\) không thể là số chính phương, bởi vì: \(n^2=n.n< n\left(n+1\right)< \left(n+1\right)\left(n+1\right)=\left(n+1\right)^2\)
tìm đa thức bậc 4 f(x) thoả mãn: f(x)-f(x-1)=x3. trình bày sơ lược cách giải. từ đó lập công thức tính tổng quát Sn=1+23+33+43+....+n3 và tính chính xác giá trị của Sn vs n=2011
phantuananh mấy tháng nữa chắc mk cũng chả cần nữa rồi
tìm đa thức bậc 4 f(x) thoả mãn: f(x)-f(x-1)=x3. trình bày sơ lược cách giải. từ đó lập công thức tính tổng quát Sn=1+23+33+43+....+n3 và tính chính xác giá trị của Sn vs n=2011
do có \(1.f\left(x\right)-1.f\left(x-1\right)=...\) nên hệ số của \(x^4\) có thể là bất kì số nào khác 0. Ta lấy là số 1 cho đơn giản.
Đặt \(f\left(x\right)=x^4+ax^3+bx^2+cx+d\)
Thay x = -1,0,1,2 (hoặc 4 số bất kì) vào \(f\left(x\right)-f\left(x-1\right)=x^3\), ta được hệ 4 ẩn, 4 pt bậc nhất, từ đó giải ra a, b, c, d.
Thay vô Sn.
tìm đa thức bậc 4 f(x) thoả mãn: f(x)-f(x-1)=x3. trình bày sơ lược cách giải. từ đó lập công thức tính tổng quát Sn=1+23+33+43+....+n3 và tính chính xác giá trị của Sn vs n=2011
Gọi F(x) = \(ax^4+bx^3+cx^2+dx+e\)
=> F(x-1) = \(a\left(x-1\right)^4+b\left(x-1\right)^3+c\left(x-1\right)^2+d\left(x-1\right)+e\)
F(x) - f(x-1) = x^3 . Rút gọn sau đó cho hệ số bằng nhau
\(Sn=1+2^3+3^3+4^3+...+n^3=\left(1+2+...+n\right)^2=\left(\frac{n\left(n-1\right)}{2}\right)^2\)
Dễ dàng cm bằng pp quy nạp
Với n = 2011 => S2011 =.....
Tính giá trị của tổng sau : \(1.2.3+2.3.4+3.4.5+...+n\left(n+1\right)\left(n+2\right)\)
Đặt A là tên biểu thức
A=1.2.3+2.3.4+...+n(n+1)(n+2)
4A=1.2.3.4+2.3.4.4+...+n(n+1)(n+2).4
4A=1.2.3.4 - 0.1.2.3 + 2.3.4.5 - 1.2.3.4 +...+ n(n+1)(n+2)(n+3) - (n-1)n(n+1)(n+2)
4A=[1.2.3.4+2.3.4.5+...+n(n+1)(n+2)(n+3)] - [0.1.2.3+1.2.3.4+...+(n-1)n(n+1)(n+2)]
4A=n(n+1)(n+2)(n+3)-0.1.2.3
A=\(\frac{n\left(n+1\right)\left(n+2\right)\left(n+3\right)}{4}\)
\(A=1.2.3+2.3.4+3.4.5+...+n\left(n+1\right)\left(n+2\right)\)
\(\Rightarrow4A=1.2.3.4+2.3.4.4+3.4.5.4+...+4n\left(n+1\right)\left(n+2\right)\)
\(\Rightarrow4A=1.2.3.4+1.2.3.\left(5-1\right)+...+n\left(n+1\right)\left(n+2\right)\left(n+3-n+1\right)\)
\(\Rightarrow4A=1.2.3.4+2.3.4.5-1.2.3.4+...+n\left(n+1\right)\left(n+2\right)\left(n+3\right)-\left(n-1\right)n\left(n+1\right)\left(n\right)\)
\(\Rightarrow4A=n\left(n+1\right)\left(n+2\right)\left(n+3\right)\)
\(\Rightarrow A=\frac{n\left(n+1\right)\left(n+2\right)\left(n+3\right)}{4}\)
Bài 1:Cho đoạn thẳng MN = 8cm,I là trung điểm của MN. Trên tia đối của tia MI lấy điểm P sao cho Mp=2cm. Trên tia đối của tia NI lấy điểm Q sao cho NQ=2cm
a)Tính độ dài đoạn thẳng PN
b)Điểm I có phải là trung điểm của đoạn thẳng không? Vì sao?
Bài 2:Tính các tổng :
a)A=7+11+15+...+203.
b)B=6+11+16+....+301.
Bài 3:Cho tổng S =5+8+11+14+.....
a)Tìm số hạng thứ 100 của tổng
b)Tính tổng 100 số hạng đầu tiên.
Min'na ga tasuketekudasai hōpu!!!
Bài 2:
A=7+11+15+....+203(SSH của tổng là:(203-7):4+1=50)
A=(7+203)X50:2
A=210X50:2
A=5250
B=6+11+16+....301(SSH của tổng là:A=(301-6):5+1=40)
B=(6+301)X40:2
B=307X20
B=6140
Bài 7:
a)Số hạng thứ 100 của tổng là:
(5+3).(100-1)=792
b)Tổng 100 sô hạng đầu tiên là:
(5+792).100:2=39850
tổng kết học kì I, tổng số học sinh giỏi khối 6 là 90 em .Biết 2/5 số học sinh giỏi của 6A =1/3 số học sinh giỏi của 6B và = 1/2 số học sinh giỏi của 6C. Tính số học sinh giỏi mỗi lớp
Gọi số học sinh giỏi của lớp 6A,6B,6C lần lượt là a,b,c
Theo đề, ta có: 2/5a=1/3b=1/2c
=>a/2,5=b/3=c/2
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{2.5}=\dfrac{b}{3}=\dfrac{c}{2}=\dfrac{a+b+c}{2.5+3+2}=\dfrac{90}{7.5}=12\)
=>a=30; b=36; c=24
cho tổng S= 7+12+17+22+...
a) Tìm số hạng thứ 50 của tổng
b)Tính tổng của 50 số hạng đầu tiên
giúp mih vs nha
a) Gọi số hạng thứ 50 của tổng là: n
Ta có:
( n - 7 ) : 5 + 1 = 50
( n - 7 ) : 5 = 50 - 1
( n - 7 ) : 5 = 49
n - 7 = 49 x 5
n - 7 = 245
n = 245 + 7
n = 252
Vậy số đó là: 252
b) Tổng của 50 số hạng đầu tiên là:
( 252 + 7 ) x 50 : 2 = 6475
Đ/S: a: 252
b: 6475