Cho lăng trụ đứng ABC. A’B’C’ có cạnh bên AA’=2a, AB=AC=a, góc B A C ^ = 120 ° . Gọi M là trung điểm của BB’ thì cosin của góc tạo bởi hai mặt phẳng (ABC) và (AC’M) là
A. 3 31
B. 3 3
C. 3 15
D. 93 31
Cho hình lăng trụ đứng ABC. A’B’C’ có tam giác ABC vuông tại A, AB= AA’=a, AC =2a . Tính thể tích khối lăng trụ đã cho
A. a 3 3
B. 2 a 3 3
C. a 3
D. 2 a 3
Cho lăng trụ đứng ABC.A'B'C' có cạnh bên AA'=2a,AB=AC =a, góc B A C ^ = 120 ° . Gọi M là trung điểm của BB' thì cosin của góc tạo bởi hai mặt phẳng (ABC) và (AC'M) là:
A. 3 31
B. 5 5
C. 3 15
D. 93 31
Đáp án D
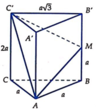
Nhận thấy ∆ A B C là hình chiếu của ∆ A M C ' lên mặt phẳng (ABC).
Gọi φ là góc giữa (AMC') và ( A B C ) ⇒ S ∆ A B C = S ∆ A M C ' . cos φ ⇒ cos φ = S ∆ A B C S ∆ A M C '
Ta có S ∆ A B C = 1 2 a 2 . sin 120 ° = a 2 3 4
A ' C = a 5 ; A M = a 2 ; B C = a 2 + a 2 - 2 a cos 120 ° = a 3 ⇒ C ' M = 2 a
Đặt p = a 5 + a 2 + 2 a 2
⇒ S ∆ A M C ' = p ( p - a 2 ) ( p - a 5 ) ( p - 2 a ) = 31 4 a 2
⇒
cos
φ
=
a
2
3
4
.
4
31
a
2
=
3
31
=
93
31
Cho lăng trụ đứng ABC A’B’C’ có đáy ABC là tam giác vuông cân tại B AB=2a cạnh bên AA’=2a căn 2 gọi M là trung điểm của cạnh BC khoảng cách giữa hai đường thẳng AM và B’C giải bài phương pháp toạ độ
Đặt hệ trục Oxyz vào lăng trụ, với gốc O trùng B, tia BA trùng Ox, tia BC trùng Oy, tia BB' trùng Oz. Quy ước a là 1 đơn vị độ dài.
Ta có tọa độ các điểm: \(A\left(2;0;0\right)\) ; \(B\left(0;0;0\right)\) ; \(C\left(0;2;0\right)\); \(B'\left(0;0;2\sqrt{2}\right)\)
Do M là trung điểm BC \(\Rightarrow M\left(0;1;0\right)\)
\(\overrightarrow{u_{AM}}=\overrightarrow{AM}=\left(-2;1;0\right)\); \(\overrightarrow{u_{B'C}}=\overrightarrow{B'C}=\left(0;2;-2\sqrt{2}\right)\)
\(\overrightarrow{AC}=\left(-2;2;0\right)\) (A là điểm thuộc đường AM, C là điểm thuộc đường B'C)
\(\left[\overrightarrow{u_{AM}};\overrightarrow{u_{B'C}}\right]=\left[-2\sqrt{2};-4\sqrt{2};-4\right]\)
Áp dụng công thức k/c hai đường chéo nhau:
\(d\left(AM;B'C\right)=\dfrac{\left|\left[\overrightarrow{u_{AM}};\overrightarrow{u_{B'C}}\right].\overrightarrow{AC}\right|}{\left|\left[\overrightarrow{u_{AM}};\overrightarrow{u_{B'C}}\right]\right|}=\dfrac{2a\sqrt{7}}{7}\) (sau khi đã đổi lại 1 đơn vị độ dài bằng a)
Bạn kiểm tra lại tính toán
Cho lăng trụ đứng ABC.A'B'C', có đáy ABC là tam giác vuông tại A, AB = 3a; AC = 4a, cạnh bên AA' = 2a. Tính thể tích của khối lăng trụ .
A. 12 a 3
B. 4 a 3
C. 3 a 3
C. 6 a 3
Cho lăng trụ đứng ABC.A'B'C', có đáy ABC là tam giác vuông tại A, AB=3a,AC=4a cạnh bên AA'=2a. Tính thể tích của khối lăng trụ ABC.A'B'C'.
A. 12 a 3
B. 4 a 3
C. 3 a 3
D. 6 a 3
Cho lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông tại A;BC = 2a, A B C ^ = 30 0 . Biết cạnh bên của lăng trụ bằng 2 a 3 . Thể tích khối lăng trụ là:
A. a 3 3
B. 6 a 3
C. 3 a 3
D. 2 a 3 3
Cho hình lăng trụ đứng tam giác ABC.A'B'C' có đáy ABC là tam giác cân, AB=AC=a, B A C ^ = 120 ∘ , cạnh bên A A ' = a 2 . Tính góc giữa hai đường thẳng AB' và BC. (tham khảo hình vẽ bên)
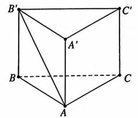
A. 90 ∘
B. 30 ∘
C. 45 ∘
D. 60 ∘
Cho lăng trụ đứng ABC.A'B'C' có cạnh bên AA' = 2a, AB = AC = a, góc B A C ^ = 120 0 . Gọi M là trung điểm của BB' thì cosin của góc tạo bởi hai mặt phẳng (ABC) và (AC'M) là:
A . 3 31
B . 5 5
C . 3 15
D . 93 31
Đáp án D.

Nhận thấy ∆ ABC là hình chiếu của ∆ AMC' lên mặt phẳng (ABC).
Gọi φ là góc giữa (AMC') và (ABC)
![]()

Ta có 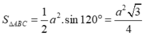
![]()
![]()
=> C'M = 2a

![]()
![]()
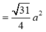
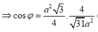
![]()
Cho lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông tại B, AB = a, AA’= 2a. Tính khoảng cách từ điểm A đến mặt phẳng (A’BC)
A. 2 5 a
B. 2 5 a 5
C. 5 a 5
D. 3 5 a 5