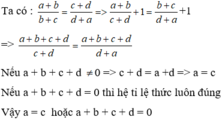Chứng minh rằng nếu a > 0 , b > 0 , c > 0 v à a < b thì a b < a + c b + c
PB
Những câu hỏi liên quan
Bài 4: Chứng minh rằng: -(a-b-c)+(-a+b-c)-(-a+b+c)=-(a-b+c)
Bài 5: Cho M=(-a+b)-(b+c-a)+(c-a) Chứng minh rằng: Nếu a<0 thì M>0
Mình cần gấp ạ!
\(4,VT=-a+b+c-a+b-c+a-b-c=-a+b-c=-\left(a-b+c\right)=VP\\ 5,M=-a+b-b-c+a+c-a=-a\\ M>0\Rightarrow-a>0\Rightarrow a< 0\)
Đúng 5
Bình luận (0)
Cho 2 số hữu tỉ a/b, e/d (b>0, d>0). Chứng minh rằng a/b<c/d nếu ad<bc và ngược lại
+) Ta có: \(\dfrac{a}{b}< \dfrac{c}{d}\Rightarrow\dfrac{ad}{bd}< \dfrac{bc}{bd}\Rightarrow ad< bc\)
( do b, d > 0 )
+) Ta có: \(ad< bc\)
\(\Rightarrow\dfrac{ad}{bd}< \dfrac{bc}{bd}\Rightarrow\dfrac{a}{b}< \dfrac{c}{d}\left(b,d>0\right)\)
Đúng 2
Bình luận (0)
Để \(\dfrac{a}{b}< \dfrac{a+c}{b+d}\) thì \(a\left(b+d\right)< b\left(a+c\right)\Leftrightarrow ab+ad< ab+bc\Leftrightarrow ad< bc\Leftrightarrow\dfrac{a}{b}< \dfrac{c}{d}\)
Để \(\dfrac{a+c}{b+d}< \dfrac{c}{d}\) thì \(\left(a+c\right).d< \left(b+d\right).c\Leftrightarrow ad+cd< bc+cd\Leftrightarrow ab< bc\Leftrightarrow\dfrac{a}{b}< \dfrac{c}{d}\)
Chúc Bạn Học Tốt !!!Đạt nhiều thành tích trong học tập
Xem lại đề nha bạn :\(\dfrac{a}{b},\dfrac{c}{d}\left(b,d>0\right)\) chứ
Đúng 0
Bình luận (0)
Bài 1:Cho 2 soos hữu tỷ a/b , c/d (b > 0 , d > 0) . Chứng minh rằng a/b < c/d nếu a/d < b/c và ngược lại.
Bài 2: Chứng minh nếu a/b < c/d (b > 0, d >0) thì : a/b < a+c/ b+d < c/d.
giúp mình với mình đang cần gấp lắm
B1: Ta có :a/b < c/d
=>ad/bd < bc/ba
=>ad < bc
Đúng 0
Bình luận (0)
Chứng minh rằng nếu a+b/b+c =c+d/d+a (c+d khác 0) thì a=c và a+b+c+d=0
Chứng minh rằng: Nếu a + b b + c = c + d d + a (c + d ≠ 0) thì a = c hoặc a = b + c + d = 0
1.a)Cho các số dương a,b,c có tích bằng 1.Chứng minh rằng (a+1)(b+1)(c+1) lớn hơn hoặc bằng 8.
b)Chocacs số a và b không âm.Chứng minh rằng (a+b)(ab+1) lớn hơn hoặc bằng 4ab.
2.Cho các số dương a,b,c,d có tích bằng 1.Chứng minh rằng a bình +b bình +c bình +d bình +ab+cd lớn hơn hoặc bằng 6.
3.Chứng minh rằng nếu a+b+c>0.abc>0.ab+bc+ca>0 thì a>0,b>0,c>0.
3. abc > 0 nên trog 3 số phải có ít nhất 1 số dương.
Vì nếu giả sử cả 3 số đều âm => abc < 0 => trái giả thiết
Vậy nên phải có ít nhất 1 số dương
Không mất tính tổng quát, giả sử a > 0
mà abc > 0 => bc > 0
Nếu b < 0, c < 0:
=> b + c < 0
Từ gt: a + b + c < 0
=> b + c > - a
=> (b + c)^2 < -a(b + c) (vì b + c < 0)
<=> b^2 + 2bc + c^2 < -ab - ac
<=> ab + bc + ca < -b^2 - bc - c^2
<=> ab + bc + ca < - (b^2 + bc + c^2)
ta có:
b^2 + c^2 >= 0
mà bc > 0 => b^2 + bc + c^2 > 0
=> - (b^2 + bc + c^2) < 0
=> ab + bc + ca < 0 (vô lý)
trái gt: ab + bc + ca > 0
Vậy b > 0 và c >0
=> cả 3 số a, b, c > 0
Đúng 0
Bình luận (0)
1.a, Ta có: \(\left(a+b\right)^2\ge4a>0\)
\(\left(b+c\right)^2\ge4b>0\)
\(\left(a+c\right)^2\ge4c>0\)
\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64abc\)
Mà abc=1
\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\left(đpcm\right)\)
Đúng 0
Bình luận (0)
sai rồi. sửa a+b=a+1, b+c=b+1, a+c=c+1 nha, thông cảm, nhìn sai đề
Đúng 0
Bình luận (0)
Chứng minh rằng nếu a + b/ b+ c = c+ d/ d+ a thì a= c hoặc a+ b+ c+ d= 0 (với c+ d# 0)Cho x/a+2b+c= y/2a+y-z = z/4a-4b+c. Chứng minh rằng : a/x+2y+z=b/ 2x+y-z = c/ 4x- 4y+ c
Xem chi tiết
( với abc # 0 và các mẫu đều khác 0)
Chứng minh rằng nếu a/b < c/d (b>0 ,d>0 ) thì a/b < a+c/b+d < c/d
Ta có : \(\frac{a}{b}0\) \(\left(1\right)\)
vì \(ad\)\(
Đúng 0
Bình luận (0)
Chứng minh rằng : Nếu a/b < c/d (b>0,d>0) thì a/b <a+c/b+d<c/d
Ta có:a/b<c/d =>ad<bc (1)
Thêm ab vào (1) ta đc:
ad+ab<bc+ab hay a(b+d)<b(a+c) =>a/b<a+c/b+d (2)
Thêm cd vào 2 vế của (1), ta lại có:
ad+cd<bc+cd hay d(a+c)<c(b+d) => c/d>a+c/b+d (3)
Từ (2) và (3) suy ra:a/b<a+c/b+d<c/d
Đúng 0
Bình luận (0)