1: I là tâm đường tròn nội tiếp

QB=QC

=>QB=QI

=>ΔQBI cân tạiQ

2: Xet ΔAMI và ΔANI có

góc AMI=góc ANI

góc MAI=góc NAI

AI chung

=>ΔAMI=ΔANI

=>góc AMN=góc ANM=90 độ-1/2*góc ABC và AM=AN

=>góc EMB=góc NMB=90 độ+1/2*gócc ABC

góc IBC=1/2*góc ABC

góc ICB=góc ACB/

=>góc EIB+góc EMB=180 độ

=>ĐPCM

Em kham khảo link này nhé.

Câu hỏi của Trần Đức Thắng - Toán lớp 9 - Học toán với OnlineMath

1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)

 ~~~~~~~~~ Bài làm ~~~~~~~~~

Ta có: \(\widehat{HBD}=\widehat{DAC}\) (Cùng phụ với \(\widehat{ACB}\))

\(\widehat{KBD}=\widehat{DAC}\)( Góc nối tiếp cùng chắn cung \(KC\))

\(\Rightarrow\widehat{HBD}=\widehat{KBD}\)

Ta lại có: \(BD\perp HK\)

\(\Rightarrow BD\) là đường trung trực của \(HK\)

\(\Rightarrow\Delta IHK\) cân tại \(I\)

\(\Rightarrow\widehat{BKD}=\widehat{BHD}=\widehat{AHQ}\)

Lại có:\(\widehat{DKO}=\widehat{HAO}\)( \(\Delta OKA\) cân tại \(O\))

Vì vậy: \(\widehat{DKO}+\widehat{BKD}=\widehat{HAO}+\widehat{AHQ}=90^0\)

\(\Rightarrow\widehat{KIO}=90^0\)

\(\Rightarrow IK\)là tiếp tuyến của đường tròn \(\left(O\right)\)

(Hình vẽ chỉ mang tính chất minh họa cái hình vẽ gần cả tiếng đồng hồ :)) )

Ủa bạn ơi sao phụ nhau? Dòng đầu ấy

Đúng rồi bạn. Phụ nhau ý nghĩa là ^HBD + ^ACB = 90^0 và tương tự như góc kia. (Tam giác vuông ý)

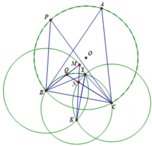
1) Ta có

  B I C ^ = 180 0 − I B C ^ − I C B ^ = 180 0 − A B C ^ 2 − A C B ^ 2 = 180 0 − 180 ∘ − B A C ^ 2 = 90 0 + B A C ^ 2 ⇔ B A C ^ = 2 B I C ^ − 180 °

Tương tự B Q C ^ = 90 0 + B P C ^ 2 ⇔ B P C ^ = 2 B Q C ^ − 180 ° .

Tứ giác BPAC nội tiếp, suy ra B A C ^ = B P C ^ ⇒ B Q C ^ = B I C ^ , nên 4 điểm B, I, Q, C thuộc một đường tròn.

2) Gọi đường tròn (B; BI) giao (C; CI) tại K khác I thì K cố định.

Góc I B M ^  là góc ở tâm chắn cung I M ⏜  và I K M ^  là góc nội tiếp chắn cung  I M ⏜ , suy ra I K M ^ = 1 2 I B M ^  (1).

Tương tự I K N ^ = 1 2 I C N ^  (2).

Theo câu 1) B, I, Q, C thuộc một đường tròn, suy ra  I B M ^ = I B Q ^ = I C Q ^ = I C N ^  (3).

Từ (1), (2) và (3), suy ra I K M ^ = I K N ^ ⇒ K M ≡ K N .

Vậy MN đi qua K cố định.

Pika...........................chịu!

>-<

1. Do BD , CE là đường cao của tam giác ABC nên \(\widehat{BDC}=90^o\)và \(\widehat{BEC}=90^o\)

Vì E , D nằm cùng 1 phía trên nửa mặt phẳng có bờ là đường thẳng BC nên tứ giác BCDE nội tiếp trong đường trong đường kính BC

2. Trên cung tròn đường kính BC ta có : \(\widehat{D_1}=\widehat{C_1}\)( cùng chắc cung \(\widebat{BE}\))

Trên đường tròn (O) , ta có : \(\widehat{M_1}=\widehat{C_1}\)( cùng chắn cung \(\widebat{BN}\))

Suy ra : \(\widehat{D_1}=\widehat{M_1}\Rightarrow MN//DE\)( do có 2 góc đồng vị bằng nhau )

3. Gọi H là trực tâm của tam giác ABC và I là trung điểm của BC.

Xét tứ giác ADHE có \(\widehat{AEH}=90^o\)( do CE vuông AB )

                                 \(\widehat{ADH}=90^o\)( do BD vuông AC )

\(\Rightarrow\widehat{AEH}+\widehat{ADH}=180^O\)nên tứ giác ADHE nội tiếp đường tròn đường kính AH

Vậy đường tròn ngoại tiếp tam giác ADE là đường tròn đường kính AH , có bán kính bằng \(\frac{AH}{2}\)

Kẻ đường kính AK của đường tròn (O) , ta có : 

\(\widehat{KBA}=90^o\)( góc nội tiếp chắn nửa đường tròn (O) )

\(\Rightarrow KB\perp AB\)

mà \(CE\perp AB\left(gt\right)\)nên KB // CH (1)

Chứng minh tương tự ta có KC // BH (2)

Từ (1) và (2) => BKCH là hình bình hành

Vì I là trung điểm của BC suy ra I cũng là trung điểm của KH . Mặt khác ta có O là trung điểm của AK nên \(OI=\frac{AH}{2}\). Do BC cố định nên I cố định suy ra Oi không đổi

Vậy khi điểm A di động trên cung lớn BC thì độ dài bán kính đường tròn ngoại tiếp tam giác ADE luôn không đổi 

Do tứ giác BCDE nội tiếp nên \(\widehat{ADE}=\widehat{ABC}\)( tính chất góc ngoài bằng góc trong đối diện ) (3)

Xét 2 tam giác ADE và ABC ta có \(\widehat{DAE}=\widehat{BAC}\), kết hợp với (3) ta có 2 tam giác này đồng dạng 

\(\Rightarrow\frac{S_{\Delta ADE}}{S_{\Delta ABC}}=\left(\frac{AD}{AB}\right)^2=\left(\cos\widehat{DAB}\right)^2=\left(\cos\widehat{CAB}\right)^2\)

Do BC cố định nên cung nhỏ BC không đổi suy ra số đô góc CAB không đổi . Vậy để S_ADE đạt giá trị lớn nhất thì S_ABC cũng phải đạt giá trị lớn nhất . Điều này xảy ra khi và chỉ khi A là điểm chính giữa cung lớn BC