Số gia của hàm số f ( x ) = x 2 2 ứng với số gia Δx của biến số x tại x 0 = - 1 là
A. 1 2 ∆ x 2 - ∆ x
B. 1 2 ∆ x 2 - ∆ x
C. 1 2 ∆ x 2 + ∆ x
D. 1 2 ∆ x 2 + ∆ x
PB
Những câu hỏi liên quan
Số gia của hàm số
f
(
x
)
x
2
ứng với số gia δx của đối số x tại
x
0
-
1
là A.
∆
x
2
-
2
∆
x
-
1
B.
∆
x
2
+
2...
Đọc tiếp
Số gia của hàm số f ( x ) = x 2 ứng với số gia δx của đối số x tại x 0 = - 1 là
A. ∆ x 2 - 2 ∆ x - 1
B. ∆ x 2 + 2 ∆ x + 2
C. ∆ x 2 + 2 ∆ x
D. ∆ x 2 - 2 ∆ x
- Với số gia của đối số x tại điểm x 0 = - 1 , ta có:
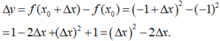
Chọn D.
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
x
2
−
x
, đạo hàm của hàm số ứng với số gia
Δ
x
của đối số x tại
x
0
là A.
lim
Δ
x
→
0
Δ
x
2...
Đọc tiếp
Cho hàm số f ( x ) = x 2 − x , đạo hàm của hàm số ứng với số gia Δ x của đối số x tại x 0 là
A. lim Δ x → 0 Δ x 2 + 2 x Δ x − Δ x .
B. lim Δ x → 0 Δ x + 2 x − 1 .
C. lim Δ x → 0 Δ x + 2 x + 1 .
D. lim Δ x → 0 Δ x 2 + 2 x Δ x + Δ x .
Cho hàm số
f
(
x
)
x
2
-
x
, đạo hàm của hàm số ứng với số gia Δx của đối số x tại
x
0
là A.
lim
∆
x
→
0
∆
x
2
+
2...
Đọc tiếp
Cho hàm số f ( x ) = x 2 - x , đạo hàm của hàm số ứng với số gia Δx của đối số x tại x 0 là
A. lim ∆ x → 0 ∆ x 2 + 2 x ∆ x - ∆ x
B. lim ∆ x → 0 ∆ x + 2 x - 1
C. lim ∆ x → 0 ∆ x + 2 x + 1
D. lim ∆ x → 0 ∆ x 2 + 2 x ∆ x + ∆ x
Cho hàm số
f
(
x
)
x
2
-
x
, đạo hàm của hàm số ứng với số gia Δx của đối số x tại
x
0
là: A.
lim
∆
x
→
0
∆
x
2
-
2...
Đọc tiếp
Cho hàm số f ( x ) = x 2 - x , đạo hàm của hàm số ứng với số gia Δx của đối số x tại x 0 là:
A. lim ∆ x → 0 ∆ x 2 - 2 x 0 ∆ x - ∆ x
B. lim ∆ x → 0 ∆ x + 2 x 0 - 1
C. lim ∆ x → 0 ∆ x + 2 x 0 + 1
D. lim ∆ x → 0 ∆ x 2 + 2 x 0 ∆ x + ∆ x
Cho hàm số
f
(
x
)
x
2
−
x
, đạo hàm của hàm số ứng với số gia
Δ
x
của đối số x tại x0 là A.
lim
Δ
x
→
0
Δ
x
2
+...
Đọc tiếp
Cho hàm số f ( x ) = x 2 − x , đạo hàm của hàm số ứng với số gia Δ x của đối số x tại x0 là
A. lim Δ x → 0 Δ x 2 + 2 x Δ x − Δ x .
B. lim Δ x → 0 Δ x + 2 x − 1 .
C. lim Δ x → 0 Δ x + 2 x + 1 .
D. lim Δ x → 0 Δ x 2 + 2 x Δ x + Δ x .
Đáp án B
Ta có
Δ y = ( x 0 + Δ x ) 2 − ( x 0 + Δ x ) − ( x 0 2 − x 0 ) = △ x 2 + 2 x 0 Δ x − Δ x .
Nên
f ' ( x 0 ) = lim Δ x → 0 Δ y Δ x = lim Δ x → 0 ( Δ x ) 2 + 2 x 0 Δ x − Δ x Δ x = lim Δ x → 0 ( Δ x + 2 x 0 − 1 ) .
Vậy f ' ( x ) = lim Δ x → 0 ( Δ x + 2 x − 1 ) .
Đúng 0
Bình luận (0)
Tính số gia của hàm số y= \(\dfrac{x^2}{2}\) tại điểm x0 =-1 ứng với số gia Δx
Số gia của hàm số f ( x ) = x 3 ứng với x 0 = 2 và Δx = 1 bằng bao nhiêu?
A.-19
B. 7
C. 19
D. -7
Số gia của hàm số f ( x ) = x 3 ứng với x 0 = 2 và Δx = 1 bằng bao nhiêu?
A. -19.
B. 7.
C. 19.
D. -7.
Đáp án C
- Ta có : x 0 + Δ x = 2 + 1 = 3 .
- Do đó, số gia của hàm số đã cho là:
Đúng 0
Bình luận (0)
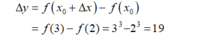
Số gia của hàm số f ( x ) = x 3 ứng với x0 = 2 và Δx = 1 bằng bao nhiêu?
A. -19
B. 7
C. 19
D. -7
