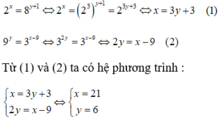(x-y)(3x-4y)=0

=>x=y hoặc 3x=4y

TH1: x=y

\(B=\dfrac{3y+4y}{5y-4y}+\dfrac{3y-8y}{5y+8y}=7+\dfrac{-5}{13}=\dfrac{86}{13}\)

TH2: 3x=4y

=>x/4=y/3=k

=>x=4k; y=3k

\(B=\dfrac{3x+4y}{5x-4y}+\dfrac{3x-8y}{5x+8y}\)

\(=\dfrac{12k+12k}{20k-12k}+\dfrac{12k-24k}{20k+24k}=\dfrac{24}{8}+\dfrac{-12}{44}=\dfrac{30}{11}\)

Vì \(3x=8y\Rightarrow\frac{x}{8}=\frac{y}{3}\Rightarrow\frac{x}{8}=\frac{2y}{6}\)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có : \(\frac{x}{8}=\frac{2y}{6}=\frac{x-2y}{8-6}=\frac{4}{2}=2\)

\(\Rightarrow x=2.8=16\)                                                  Thử lại : \(3x=16\times3=48\)

\(\Rightarrow y=2.6\div2=6\)                                                           \(8y=6\times8=48\)

Vậy  \(x=16;y=6\)

Vì \(3x=2y\)nên:

\(\Rightarrow\frac{x}{2}=\frac{y}{3}\)

Ta thấy: \(\frac{y}{3}=\frac{2y}{6}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

          \(\frac{x}{2}=\frac{y}{3}=\frac{2y}{6}=\frac{x-2y}{6-4}=\frac{4}{2}=2\)

\(\Rightarrow x=2.2=4\)

\(\Rightarrow y=2.3=6\)

Theo bài ra ta có: 

\(3x=8y\)\(\Rightarrow\frac{x}{8}=\frac{y}{3}\)\(\Rightarrow\frac{x}{8}=\frac{2y}{6}\)

Áp dụng tính chất dãy tỉ số bằng nhau và giả thiết ta có:

\(\frac{x}{8}=\frac{2y}{6}=\frac{x-2y}{8-6}=\frac{4}{2}=2\)

\(\Rightarrow\hept{\begin{cases}x=2.8=16\\2y=2.6=12\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}x=16\\y=6\end{cases}}\)

Ta có: \(\dfrac{x-1}{6}=\dfrac{-2y+3}{30}\)

\(\Leftrightarrow\dfrac{3x-3}{18}=\dfrac{-8y+12}{120}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{3x-3}{18}=\dfrac{-8y+12}{120}=\dfrac{3x-3+8y-12}{18-120}=\dfrac{2-15}{-102}=\dfrac{13}{102}\)

Do đó: 

\(\left\{{}\begin{matrix}\dfrac{x-1}{6}=\dfrac{13}{102}\\\dfrac{3-2y}{30}=\dfrac{13}{102}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-1=\dfrac{13}{17}\\-2y+3=\dfrac{65}{17}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{30}{17}\\-2y=\dfrac{14}{17}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{30}{17}\\y=\dfrac{-7}{17}\end{matrix}\right.\)

Ta có: 5x - 5 = 3 - 2y

=> 5x+2y = 8

=> 20x + 8y = 32

Mà 3x +8y = 2

=> 17x = 30

=> x = \(\dfrac{30}{7}\)

=> y = ... giải tiếp nha bạn.

Xin 1 like nha bạn. Thx bạn

Vậy x + y =27.

Chọn đáp án D.

a: \(A=x^2+2xy+y^3=5^2+2\cdot5\cdot4+4^3=129\)

b: \(B=\left(-1\right)\cdot\left(-1\right)-\left(-1\right)^2\cdot\left(-1\right)^2+\left(-1\right)^4\cdot\left(-1\right)^4-\left(-1\right)^6\cdot\left(-1\right)^6=1-1+1-1=0\)

\(a)xy+3x-2y=11\)

\(\Leftrightarrow xy+3x-2y-6=5\)

\(\Leftrightarrow x\left(y+3\right)-2\left(y+3\right)=5\)

\(\Leftrightarrow\left(y+3\right)\left(x-2\right)=5\)

\(\Leftrightarrow\hept{\begin{cases}y+3=-1\\x-2=-5\end{cases}}\Leftrightarrow\hept{\begin{cases}y=-4\\x=-3\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}y+3=1\\x-2=5\end{cases}}\Leftrightarrow\hept{\begin{cases}y=-2\\x=7\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}y+3=-5\\x-2=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}y=-8\\x=1\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}y+3=5\\x-2=1\end{cases}}\Leftrightarrow\hept{\begin{cases}y=2\\x=3\end{cases}}\)

\(b)2x^2-2xy+x-y=12\)

\(\Leftrightarrow2x\left(x-y\right)+\left(x-y\right)=12\)

\(\Leftrightarrow\left(x-y\right)\left(2x+1\right)=12\)

\(\Rightarrow\left(x-y\right);\left(2x+1\right)\inƯ\left(12\right)\)

\(\RightarrowƯ\left(12\right)\in\left\{-1;1;-2;2;-3;3;-4;4;-6;6;-12;12\right\}\)

Vì 2x+1 luôn lẻ

\(\Rightarrow2x+1\in\left\{-1;1;-3;3\right\}\)

\(\Leftrightarrow\hept{\begin{cases}2x+1=-1\\x-y=-12\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=11\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}2x+1=1\\x-y=12\end{cases}}\Leftrightarrow\hept{\begin{cases}x=0\\y=-12\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}2x+1=-3\\x-y=-4\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-2\\y=2\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}2x+1=3\\x-y=4\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=-3\end{cases}}\)

\(c)2xy-10y-x=13\)

\(\Leftrightarrow x\left(2y-1\right)-2y.5+5=18\)

\(\Leftrightarrow x\left(2y-1\right)-5\left(2y-1\right)=18\)

\(\Leftrightarrow\left(2y-1\right)\left(x-5\right)=18\)

\(\Leftrightarrow2y-1;x-5\inƯ\left(18\right)\)

\(\RightarrowƯ\left(18\right)\in\left\{-1;1;-2;2;-3;3;-6;6;-9;9;-18;18\right\}\)

Vì 2y-1  luôn lẻ

=>2y-1 thuộc {-1;1;-3;3;-9;9}

=> Làm  tương tự nhé

\(e)xy-2y^2+8y-3x=13\)

\(\Leftrightarrow xy-2y^2+2y+6y-3x-6=7\)

\(\Leftrightarrow y\left(x-2y+2\right)+3\left(-x+2y-2\right)=7\)

\(\Leftrightarrow y\left(x-2y+2\right)-3\left(x-2y+2\right)=7\)

\(\Leftrightarrow\left(x-2y+2\right)\left(y-3\right)=7\)

Tự khai triển như các câu trên.

Mình đg bận nên ko lm đc hết câu.

1. Ta có: \(3x=8y\)=> \(\frac{x}{8}=\frac{y}{3}\)=> \(\frac{x}{8}=\frac{2y}{6}\)

Áp dụng t/c của dãy tỉ số bằng nhau, ta có:

 \(\frac{x}{8}=\frac{2y}{6}=\frac{x-2y}{8-6}=\frac{4}{2}=2\)

=> \(\hept{\begin{cases}\frac{x}{8}=2\\\frac{y}{3}=2\end{cases}}\) => \(\hept{\begin{cases}x=2.8=16\\y=2.3=6\end{cases}}\)

Vậy x = 16 và y = 6

2. xem lại đề

3x = 8y và x - 2y = 4 . Tìm x và y

3x = 8y

\(\Rightarrow\frac{x}{8}=\frac{y}{3}\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có :

\(\frac{x}{8}=\frac{y}{3}=\frac{2y}{6}=\frac{x-2y}{8-2}=\frac{4}{2}=2\)

Từ \(\frac{x}{8}=2\Rightarrow x=16\)

\(\frac{2y}{6}=2\Rightarrow2y=12\Rightarrow y=6\)

Vậy x= 16 và y = 6

 \(\frac{x}{5}=\frac{y}{6};\frac{y}{8}=\frac{z}{11}\)

\(\Leftrightarrow\frac{x}{5}=\frac{y}{6}\Rightarrow\frac{x}{5}.\frac{1}{8}=\frac{y}{6}.\frac{1}{8}\Rightarrow\frac{x}{40}=\frac{y}{48}\left(1\right)\)

\(\Leftrightarrow\frac{y}{8}=\frac{z}{11}\Rightarrow\frac{y}{8}.\frac{1}{6}=\frac{z}{11}.\frac{1}{6}\Rightarrow\frac{y}{48}=\frac{z}{66}\left(2\right)\)

Từ ( 1 ) và ( 2 ) \(\Rightarrow\frac{x}{40}=\frac{y}{48}=\frac{z}{66}\)

Áp dụng tính chát của dãy tỉ số bằng nhau ta có :

Em tự thay số vào mà tính nha

Study well 

1, \(2x^2+4x=2x\left(x+2\right)\)

2, \(15x^3+5x^2-10x=5x\left(3x^2+x-2\right)=5x\left(x-\dfrac{2}{3}\right)\left(x+1\right)\)

3) \(5x^2\left(x-2y\right)+15x\left(x-2y\right)=\left(5x^2+15x\right)\left(x-2y\right)=5x\left(x+3\right)\left(x-2y\right)\)

4) \(3\left(x-y\right)+5x\left(y-x\right)=\left(x-y\right)\left(3-5x\right)\)

5) \(5x^2-10x=5x\left(x-2\right)\)

6) \(3x-6y=3\left(x-2y\right)\)

7) \(25x^2+5x^3+x^2y=x^2\left(25+5x+y\right)\)

8) \(14x^2y-21xy^2+28x^2y^2=7xy\left(2x-3y+4xy\right)\)

9) \(x\left(y-1\right)-y\left(y-1\right)=\left(x-1\right)\left(y-1\right)\)

10) \(10x\left(x-y\right)-8y\left(y-x\right)=\left(10x+8y\right)\left(x-y\right)=2\left(5x+4y\right)\left(x-y\right)\)

\(1,=2x\left(x+2\right)\\ 2,=5x\left(3x^2+x-2\right)\\ 3,=\left(x-2y\right)\left(5x^2+15x\right)=5x\left(x+3\right)\left(x-2y\right)\\ 4,=\left(x-y\right)\left(3-5x\right)\\ 5,=5x\left(x-2\right)\\ 6,=3\left(x-2y\right)\\ 7,=5x^2\left(5+x+y\right)\\ 8,=7xy\left(2x-3y+4xy\right)\\ 9,=\left(y-1\right)\left(x-y\right)\\ 10,=\left(x-y\right)\left(10x+8y\right)=2\left(5x+4y\right)\left(x-y\right)\)