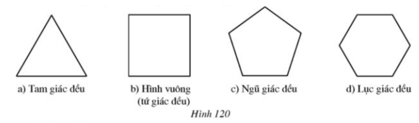
Hãy vẽ các trục đối xứng và tâm đối xứng của mỗi hình 120a, b, c, d (nếu có)
PB
Những câu hỏi liên quan
vẽ hình vuông ABCD. hãy vẽ các trục đối xứng tâm đối xứng và tâm đối xứng O của hình vuông đó
Trục đối xứng,tâm đối xứng và tâm đối xứng O của hình vuông
Đúng 0
Bình luận (0)
Vẽ hình vuông ABCD. Hãy vẽ các trục đối xứng , tâm đối xứng của nó
Số phát biểu sai:a) Phép đối xứng trục là một phép dời hìnhb) Đường thẳng d được gọi là trục đối xứng của hình (H) nếu phép đối xứng trục Đd biến hình (H) thành chính nó.c) Một hình có thể có một hay nhiều trục đối xứng, có thể không có trục đối xứng.d) Qua phép đối xứng trục, đoạn thẳng AB biến thành đoạn thẳng song song và bằng nó.e) Qua phép đối xứng trục Đa, đường tròn có tâm nằm trên a sẽ biến thành chính nó.f) Qua phép đối xứng trục Đa, tam giác có một đỉnh nằm trên a sẽ biến thành chính n...
Đọc tiếp
Số phát biểu sai:
a) Phép đối xứng trục là một phép dời hình
b) Đường thẳng d được gọi là trục đối xứng của hình (H) nếu phép đối xứng trục Đd biến hình (H) thành chính nó.
c) Một hình có thể có một hay nhiều trục đối xứng, có thể không có trục đối xứng.
d) Qua phép đối xứng trục, đoạn thẳng AB biến thành đoạn thẳng song song và bằng nó.
e) Qua phép đối xứng trục Đa, đường tròn có tâm nằm trên a sẽ biến thành chính nó.
f) Qua phép đối xứng trục Đa, tam giác có một đỉnh nằm trên a sẽ biến thành chính nó
g) Qua phép đối xứng trục Đa, ảnh của đường thẳng vuông góc với a là chính nó
h) Nều phép đối xứng trục biến đường thẳng a thành đường thẳng b cắt a thì giao điểm của a và b nằm trên trục đối xứng
i) Hình chữ nhật có 4 trục đối xứng
A. 3
B.5
C. 7
D.9
Đáp án A
Nhữngphát biểu sai: d; f; i
d) Qua phép đối xứng trục, đoạn thẳng AB biến thành đoạn thẳng song song và bằng nó hoặc là chính nó.
f) Qua phép đối xứng trục Đa, tam giác có một đỉnh nằm trên a sẽ biến thành chính nó ( chỉ trong trường hợp tam giác đều hoặc tam giác cân cóđỉnh nằm trên trục đối xứng)
i) Hình chữ nhật có 2 trục đối xứng
Đúng 0
Bình luận (0)
vẽ tâm đối xứng , trục đối xứng của tam giác cân , tam giác đều ( nếu không có thì hãy chỉ rõ và giải thích )
SGK ... Tam giác cân không có tâm đối xứng đâu... Trục đối xứng của tam giác cân là ... Khó nói quá . VD nha : tam giác ABC cân tại A TH1 : kẻ AH vuông góc với BC => AH là trục đối xứng ( CM được tam giác ABH = ACH => ĐPCM) (1)
TH2 : Kẻ trung tuyến AI vì tam giác ABC cân tại A nên => AI vừa là trung tuyến vừa là đường cao => Tương tự (1)
Nhớ được các trường hợp đặc biệt của các đường trung tuyến, phân giác, đường cao ..v..v... trong tam giác cân thì cứ biện luận thôi, không cần phải giải thích nhiều vì ta công nhận điều đó là đúng ...
Đúng 0
Bình luận (0)
Trong các hình 48, 49, 50, hình nào có trục đối xứng? Nếu là hình có trục đối xứng, hãy chỉ ra trục đối xứng của hình đó (kể cả màu sắc và họa tiết).
Xem thêm câu trả lời
Trong hình 51, các hình từ a) đến c), hình nào có trục đối xứng? Nếu là hình có trục đối xứng, hãy chỉ ra trục đối xứng của hình đó, kể cả màu sắc.
Các phát biểu nào sai?
A. Hình tròn có vô số trục đối xứng và 1 tâm đối xứng
B. Hình vuông có 4 trục đối xứng
C. Hình tam giác đều có 3 trục đối xứng 1 tâm đối xứng
D. Hình lục giác đều có 1 tâm đối xứng và 6 trục đối xứng
Các phát biểu về đối xứng hình học như sau:
A. Hình tròn: Hình tròn có vô số trục đối xứng và 1 tâm đối xứng. Điều này đúng.
B. Hình vuông: Hình vuông có 4 trục đối xứng, tương ứng với 4 đường đối xứng qua các đỉnh của hình vuông. Điều này cũng đúng.
C. Hình tam giác đều: Hình tam giác đều có 3 trục đối xứng và 1 tâm đối xứng. Điều này cũng đúng.
D. Hình lục giác đều: Hình lục giác đều có 1 tâm đối xứng và 6 trục đối xứng, tương ứng với 6 đường đối xứng qua các đỉnh của hình lục giác đều. Điều này cũng đúng.
Vậy tất cả các phát biểu đều đúng. 😊
Đúng 0
Bình luận (0)
Cho các mệnh đề sau:
1. Tam giác đều có 3 trục đối xứng và 1 tâm đối xứng
2. Hình vuông có 4 trục đối xứng và 1 tâm đối xứng
3. Ngũ giác đều có 5 trục đối xứng và 1 tâm đối xứng
4. Lục giác đều có 6 trục đối xứng và 1 tâm đối xứng
Số mệnh đềđúng là:
A.1
B.2
C.3
D.4
PL
28 tháng 11 2018 lúc 20:32
Các tứ giác sau có bao nhiêu trục đối xứng, bao nhiêu tâm đối xứng?Tứ giác: ___ trục đối xứng, ___ tâm đối xứngHình thang: ___ trục đối xứng, ___ tâm đối xứngHình thang cân: ___ trục đối xứng, ___ tâm đối xứngHình binh hành: ___ trục đối xứng, ___ tâm đối xứngHình chữ nhật: ___ trục đối xứng, ___ tâm đối xứngHình thoi: ___ trục đối xứng, ___ tâm đối xứngHình vuông: ___ trục đối xứng, ___ tâm đối xứng
Đọc tiếp
Các tứ giác sau có bao nhiêu trục đối xứng, bao nhiêu tâm đối xứng?
Tứ giác: ___ trục đối xứng, ___ tâm đối xứng
Hình thang: ___ trục đối xứng, ___ tâm đối xứng
Hình thang cân: ___ trục đối xứng, ___ tâm đối xứng
Hình binh hành: ___ trục đối xứng, ___ tâm đối xứng
Hình chữ nhật: ___ trục đối xứng, ___ tâm đối xứng
Hình thoi: ___ trục đối xứng, ___ tâm đối xứng
Hình vuông: ___ trục đối xứng, ___ tâm đối xứng
Tứ giác: 0 trục, 0 tâm
Hình thang 0 trục, 0 tâm
Hình thang cân 1 trục 0 tâm
Hình bình hành 0 trục 1 tâm
Hình chữ nhật 2 trục 1 tâm
Hình thoi 2 trục 1 tâm
Hình vuông 4 trục 1 tâm
Đúng 2
Bình luận (0)
Tứ giác: 0 trục đối xứng, 0 tâm đối xứng
Hình thang: 0 trục đối xứng, 0 tâm đối xứng
Hình thang cân: 1 trục đối xứng, 0 tâm đối xứng
Hình bình hành: 0 trục đối xứng, 1 tâm đối xứng
Hình chữ nhật: 2 trục đối xứng, 1 tâm đối xứng
Hình thoi: 2 trục đối xứng, 1 tâm đối xứng
Hình vuông: 4 trục đối xứng, 1 tâm đối xứng
Tích đúng 5 sao cho mình nhé.
OK bạn
Đúng 2
Bình luận (0)