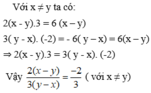Chứng minh các đẳng thức sau 4 x - 5 x y = 8 x 2 - 4 x - 10 x 2 y + 5 x y
PB
Những câu hỏi liên quan
Chứng minh đẳng thức sau :
a)(x+y).(x^4-x^3y+x^2y^2-xy^3+y^4)=x^5+y^5
\(\left(x+y\right)\left(x^4-x^3y+x^2y^2-xy^3+y^4\right)\)
\(=x^5-x^4y+x^3y^2-x^2y^3+xy^4+x^4y-x^3y^2+x^2y^3-xy^4+y^5\)
\(=\left(x^5+y^5\right)+\left(x^4y-x^4y\right)+\left(x^3y^2-x^3y^2\right)+\left(x^2y^3-x^2y^3\right)+\left(xy^4-xy^4\right)\)
\(=x^5+y^5\)
Đúng 0
Bình luận (0)
chứng minh các đẳng thức sau:
x^5- 1/ x-1= x^4+ x^3+ x^2+ x+ 1
x^5- 1/ x-1= x^4+ x^3+ x^2+ x+ 1
<=> x^5 - 1 = (x - 1)(x^4 + x^3 + x^2 + x + 1)
<=> x^5 - 1 = x^5 + x^4 + x^3 + x^2 + x - x^4 - x^3 - x^2 - x - 1
<=> x^5 - 1 = x^5 - 1 (đúng)
=> đpcm
Chứng minh các đẳng thức sau: 2 ( x - y ) 3 ( y - x ) = - 2 3 ( v ớ i x ≠ y )
chứng minh các đẳng thức sau
a) (x-y)(x^4+x^3y+x^2y^2+xy^3+y^4)= x^5-y^5
b) (x+y)(x^4-x^3y+x^2y^2-xy^3+y^4)= x^5+y^5
c) (a+b)(a^3-a^2b+ab^2-b^3)=a^4-b^4
chứng minh các đẳng thức sau
(x+y)2+(x-y)2=2(x2+y2)
\(\left(x+y\right)^2+\left(x-y\right)^2=2\left(x^2+y^2\right)\)
\(\Leftrightarrow x^2+2xy+y^2+x^2-2xy=2\left(x^2+y^2\right)\)
\(\Leftrightarrow2x^2+2y^2=2\left(x^2+y^2\right)\left(đúng\right)\)
Đúng 1
Bình luận (0)
chứng minh các đẳng thức sau
(x+y)2+(x-y)2=2(x2+y2)
Chứng minh các bất đẳng thức sau: \(\dfrac{x}{y}+\dfrac{y}{x}\ge2\left(\forall x,y>0\right)\)
Biến đổi tương đương:
\(\Leftrightarrow\dfrac{x^2+y^2}{xy}\ge2\)
\(\Leftrightarrow x^2+y^2\ge2xy\)
\(\Leftrightarrow x^2+y^2-2xy\ge0\)
\(\Leftrightarrow\left(x-y\right)^2\ge0\) (luôn đúng)
Vậy BĐT đã được chứng minh
Đúng 5
Bình luận (0)
Cách khác so với anh Nguyễn Việt Lâm
Ta có: \(\dfrac{x}{y}+\dfrac{y}{x}\ge2\sqrt{\dfrac{x}{y}\cdot\dfrac{y}{x}}=2\) (đpcm)
Đúng 1
Bình luận (0)
Chứng minh các hằng đẳng thức sau: \(x^4+y^4+\left(x+y\right)^4=2\left(x^2+xy+y^2\right)^2\)
Chứng minh vế trái bằng vế phải:
\(x^4+y^4+\left(x+y\right)^4=2x^4+2y^4+4x^3y+4xy^3+6x^2y^2\)
\(=2\left(x^4+y^4+2x^3y+2xy^3+3x^2y^2\right)\)
\(=2\left(x^4+y^4+x^2y^2+2x^3y+2xy^3+2x^2y^2\right)\)
\(=2\left(x^2+y^2+xy\right)^2\)
Đúng 0
Bình luận (0)
\(\text{Chứng minh vế trái bằng vế phải: }\)
\(x^4+y^4+\left(x+y\right)^4=2x^4+2y^4+4x^3y+4xy^3+6x^2y^2\)
\(=2\left(x^4+y^4+2x^3y+2xy^3+3x^2y^2\right)\)
\(=2\left(x^4+y^4+x^2y^2+2x^3y+2xy^3+2x^2y^2\right)\)
\(=2\left(x^2+y^2+xy\right)^2\)
Đúng 0
Bình luận (0)
Chứng minh các bất đẳng thức sau với x, y, z > 0
Chứng minh các đẳng thức sau:a)
1
x
+
2
2
x
−
1
2
x
2
+
3
x
−
2
với x
≠
-2 và x
≠
1...
Đọc tiếp
Chứng minh các đẳng thức sau:
a) 1 x + 2 = 2 x − 1 2 x 2 + 3 x − 2 với x ≠ -2 và x ≠ 1 2
b) y 2 − 5 y + 4 y − 4 = y 2 − 3 y + 2 y − 2 với y ≠ 2 và y ≠ 4.