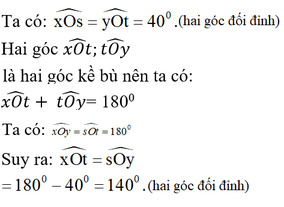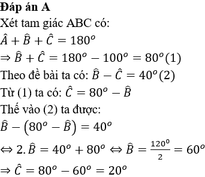Vẽ góc xOl có số đo bằng 40o
PB
Những câu hỏi liên quan
Vẽ góc xOl có số đo bằng \(40^0\) ?
cho tan giác vuông ở A, C = 40o. vẽ phân giác AD đường cao AH. tính số đo góc HAD
cho góc bẹt AOB.Trên cùng một nửa mặt phẳng bờ AB,vẽ các tia OC;ODsao cho AOC50o và góc BOD40o a) tính số đo góc BOC b) hãy chứng tỏ rằng OD và OC là hai đường thẳng vuông góc
Đọc tiếp
cho góc bẹt AOB.Trên cùng một nửa mặt phẳng bờ AB,vẽ các tia OC;ODsao cho AOC=50o và góc BOD=40o a) tính số đo góc BOC b) hãy chứng tỏ rằng OD và OC là hai đường thẳng vuông góc
cho hai góc kề bù xOy và yOy, biết xOy =40o . Vẽ tia phân giác Ot của góc yOz. Số đo của góc xOt là................độ
Sai đề rồi bạn! Làm j có thế có 2 tia Oy Hình chỉ minh họa thôi nhé!
Đúng 0
Bình luận (0)
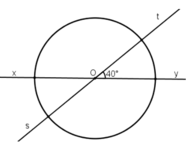
Cho hai đường thẳng xy và st cắt nhau tại O, trong các góc tạo thành có góc 40o. Vẽ một đường tròn tâm O. Tính số đo của các góc ở tâm xác định bởi hai trong bốn tia gốc O.
Cho tam giác ABC có góc B = 40o, góc C = 60o, đường trung tuyến AM. Tính số đo góc AMC.
Tam giác ABC có
A
^
100
o
,
B
^
-
C
^
40
o
. Số đo góc B và góc C lần lượt là: A.
B
^
60
°
,
C
^
20
°
B.
B
^...
Đọc tiếp
Tam giác ABC có A ^ = 100 o , B ^ - C ^ = 40 o . Số đo góc B và góc C lần lượt là:
A. B ^ = 60 ° , C ^ = 20 °
B. B ^ = 20 ° , C ^ = 60 °
C. B ^ = 70 ° , C ^ = 20 °
D. B ^ = 80 ° , C ^ = 30 °
Trên cùng một nửa mặt phẳng bờ chứa tia Oa, vẽ hình Ob, Oc sao cho aOb = 40o, aOc = 140o.
a. Tính số đo góc bOc
b. Vẽ tia Od là tia đối của tia Oc. Tia Oa có phải là tia phân giác của bOd không ? Vì sao ?
a) Ta có : aOb < aOc ( \(40^o< 140^o\))
⇒ Ob nằm giữa Oa và Oc
⇒ aOb + bOc = aOc
⇒ bOc = aOc - aOb = \(140^o-40^o=100^o\)
b) Có : Od là tia đối của Oc ⇒ Ob nằm giữa Oc và Od
⇒ dOb + bOc = \(180^o\) ( 2 góc kề bù )
⇒ dOb = \(180^o\) - bOc = \(180^o-100^o=80^o\)
Lại có : bOd > bOa ( \(80^o>40^o\))
⇒ Oa nằm giữa Ob và Od
⇒ dOa + aOb = dOb
⇒ dOa = dOb - aOb = \(80^o-40^o=40^o\)
mà aOb = \(40^o\)(gt)
⇒ Tia Oa là tia phân giác của bOd
Đúng 2
Bình luận (0)
Giải:
a) Vì +)Ob;Oc cùng ∈ 1 nửa mặt phẳng bờ chứa tia Oa
+)\(a\widehat{O}b< a\widehat{O}c\) (40o<140o)
⇒Ob nằm giữa Oa và Oc
⇒\(a\widehat{O}b+b\widehat{O}c=a\widehat{O}c\)
\(40^o+b\widehat{O}c=140^o\)
\(b\widehat{O}c=140^o-40^o\)
\(b\widehat{O}c=100^o\)
b) Vì Od là tia đối của Oc
⇒\(c\widehat{O}d=180^o\)
⇒\(d\widehat{O}b+b\widehat{O}c=180^o\)
\(d\widehat{O}b+100^o=180^o\)
\(d\widehat{O}b=180^o-100^o\)
\(d\widehat{O}b=80^o\)
⇒\(b\widehat{O}a+a\widehat{O}d=b\widehat{O}d\)
\(40^o+a\widehat{O}d=80^o\)
\(a\widehat{O}b=80^o-40^o\)
\(a\widehat{O}b=40^o\)
Vì +) \(b\widehat{O}a+a\widehat{O}d=b\widehat{O}d\)
+) \(b\widehat{O}a=a\widehat{O}d=40^o\)
⇒Oa là tia p/g của \(b\widehat{O}d\)
Chúc bạn học tốt!
Đúng 1
Bình luận (0)
Cho và là hai góc có cạnh tương ứng vuông góc. Biết góc A - góc B = 40o, tính số đo các góc A và B