Bất phương trình ax + b > 0 vô nghiệm khi
A. a ≠ 0 b = 0
B. a > 0 b > 0
C. a = 0 b ≠ 0
D. a = 0 b ≤ 0
PB
Những câu hỏi liên quan
Bất phương trình ax + b ≤ 0 vô nghiệm khi? A.
a
0
b
0
B.
a
0
b...
Đọc tiếp
Bất phương trình ax + b ≤ 0 vô nghiệm khi?
A. a = 0 b > 0
B. a > 0 b > 0
C. a = 0 b ≠ 0
D. a = 0 b ≤ 0
Nếu a > 0 thì ax + b ≤ 0 ⇔ x ≤ - b/a nên S ≠ Ø
Nếu a < 0 thì ax + b ≤ 0 ⇔ x ≥ - b/a nên S ≠ Ø
Nếu a = 0 thì ax + b ≤ 0 có dạng 0x + b ≤ 0
Với b ≤ 0 thì S = R.
Với b > 0 thì S = Ø
Chọn đáp án A.
Đúng 0
Bình luận (0)
Bất phương trình ax + b 0 vô nghiệm khi A.
a
≠
0
b
0
B.
a
0
b
0...
Đọc tiếp
Bất phương trình ax + b > 0 vô nghiệm khi
A. a ≠ 0 b = 0
B. a > 0 b > 0
C. a = 0 b ≠ 0
D. a = 0 b ≤ 0
Nếu a > 0 thì ax + b > 0 ⇔ x > - b/a nên
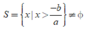
Nếu a < 0 thì ax + b > 0 ⇔ x < - b/a nên
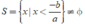
Nếu a = 0 thì ax + b > 0 có dạng 0x + b > 0
Với b > 0 thì S = R.
Với b ≤ 0 thì S = Ø
Chọn đáp án D.
Đúng 0
Bình luận (0)
Viết chương trình giải phương trình ax + b = 0 (các hệ số a,b được nhập từ bàn phím)
Hướng dẫn có sẵn trong bài là:
- Nếu a khác 0 thì phương trình có nghiệm x=-b/a(âm b phần a)
- Nếu a = 0 và b = 0 thì phương trình có vô số nghiệm
- Nếu a = 0 và b khác 0 thì phương trình vô nghiệm
uses crt;
var a, b: logint;
Begin
write('nhap so a ='); Readln(a);
write('nhap so b ='); readln(b);
If (a = 0 and b = 0)
then write ('pt co nghiem x thuoc R')
else
if (a=0 and b#0) then write('pt vo nghiem')
else
write(nghiẹm la x=': -b/a);
readln
end.
Đúng 1
Bình luận (3)
uses crt;
var a, b: logint;
Begin
write('nhap so a ='); Readln(a);
write('nhap so b ='); readln(b);
If (a = 0 and b = 0)
then write ('pt co nghiem x thuoc R')
else
if (a=0 and b#0) then write('pt vo nghiem')
else
write(nghiẹm la x=': -b/a);
readln
end.
Đúng 0
Bình luận (4)
Hệ phương trình
a
x
+
b
y
c
a
x
+
b
y
c...
Đọc tiếp
Hệ phương trình a x + b y = c a ' x + b ' y = c ' (các hệ số a’; b’; c’ khác 0) vô số nghiệm khi?
A. a a ' ≠ b b '
B. a a ' = b b ' = c c '
C. a a ' = b b ' ≠ c c '
D. b b ' ≠ c c '
Hệ phương trình a x + b y = c a ' x + b ' y = c ' có vô số nghiệm khi d: ax + by = c và d’: a’x + b’y = c’ trùng nhau, suy ra hệ phương trình có vô số nghiệm ⇔ a a ' = b b ' = c c '
Đáp án: B
Đúng 0
Bình luận (0)
viết phương trình python tìm nghiệp của phương trình ax+b=0 với a, b là hai số nguyên được nhập từ bàn phím. In ra " phương trình vô số nghiệm", " phương trình vô nghiệm" cho các trường hợp tương ứng. Nếu có nghiệm thì lấy 4 chữ số sau dấu phẩy
cho a,b,c là 3 số dương có tổng bằng 12
chứng minh rằng trong 3 phương trình :
x^2 + ax + b =0
x^2+bx+c = 0
x^2 + cx +a =0
có một phương trình vô nghiệm , một phương trình có nghiệm
Các giải của các bài toán này là sử dụng tổng các delta em nhé
Đúng 0
Bình luận (0)
Cho hệ bất phương trình
mx
+
2
m
0
2
x
+
3
5...
Đọc tiếp
Cho hệ bất phương trình mx + 2 m > 0 2 x + 3 5 > 1 - 3 x 5
Xét các mệnh đề sau:
(I) Khi m< 0 thì hệ bất phương trình đã cho vô nghiệm.
(II) Khi m= 0 thì hệ bất phương trình đã cho có tập nghiệm là R
(III) Khi m≥ 0 thì hệ bất phương trình đã cho có tập nghiệm là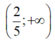 
(IV) Khi m> 0 thì hệ bất phương trình đã cho có tập nghiệm là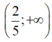 
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng ?
A. 1
B. 0
C. 2
D. 3
Cho hệ bất phương trình
mx
+
2
m
0
2
x
+
3
5...
Đọc tiếp
Cho hệ bất phương trình mx + 2 m > 0 2 x + 3 5 > 1 - 3 x 5
Xét các mệnh đề sau:
(I) Khi m< 0 thì hệ bất phương trình đã cho vô nghiệm.
(II) Khi m= 0 thì hệ bất phương trình đã cho có tập nghiệm là R.
(III) Khi m ≥ 0 thì hệ bất phương trình đã cho có tập nghiệm là 2 5 ; + ∞
(IV) Khi m > 0 thì hệ bất phương trình đã cho có tập nghiệm là 2 5 ; + ∞
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng ?
A. 1
B. 0
C. 2
D. 3
Tìm a để hệ phương trình ax + y=0, 3x+4y=0. có vô số nghiệm, vô nghiệm