Cho tam giác ABC vuông tại A, đường phân giác BD. Tính AB, BC biết AD = 4 cm và DC = 5 cm.
PB
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường phân giác BD. Tính AB, BC biết AD = 4 cm và DC = 5 cm.
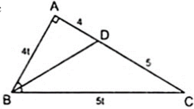
Áp dụng tính chất đường phân giác BD của tam giác ABC, ta có:
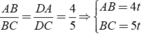với t > 0
Áp dụng định lý Py – ta – go ta có:
Khi đó: AB = 12cm, BC = 15cm
Đúng 3
Bình luận (0)
Cho tam giác ABC vuông tại A có đường phân giác BD biết AD = 3 cm BC = 5 cm Tính độ dài AB,BC
Lời giải:
Áp dụng tính chất tia phân giác:
$\frac{AD}{DC}=\frac{AB}{BC}$
$\Leftrightarrow \frac{3}{DC}=\frac{AB}{5}$
$\Rightarrow 15=AB.DC=AB(AC-AD)=AB(AC-3)(1)$
Mà: $AB^2+AC^2=BC^2=25(2)$
Từ $(1); (2)\Rightarrow (\frac{15}{AC-3})^2=AB^2=25-AC^2$
$\Leftrightarrow AC^4-6AC^3-16AC^2+150AC=0$
$\Leftrightarrow AC^3-6AC^2-16AC+150=0$
PT giải ra số khá xấu. Bạn xem lại đề.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH phân giác AD biết BC = 5 cm DC = 20 cm Tính độ dài AB AC HB HC và diện tích tam giác AHD
DB/DC=AB/DC
DB+DC=BC
=>DB=5-20=-15 là sai đề rồi bạn
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH phân giác AD biết BC = 5 cm DC = 20 cm Tính độ dài AB AC HB HC và diện tích tam giác AHD
Xem chi tiết
Cho tam giác ABC có AB = 4 cm, AC = 5 cm, BC = 6 cm, các đường phân giác BD và CE cắt nhau tại I.
a) Tính độ dài AD, DC
b) tính độ dài AE, BE.
cho tam giác abc vuông tại b, phân giác ad (d thuộc bc). Qua d kẻ đường thẳng vuông góc với ac tại f.
a, tính bc biết ab=3cm,ac=5cm
b, CM:tam giác bad= tam giác fad
c, CM: ad là trung trực của bf; bd<dc
Cho tam giác ABC vuông tại a có AB bằng 6 cm AC bằng 8 cm đường cao AH và đường phân giác BD cắt nhau tại I a) tính AC AD và DC b) chứng minh hai tam giác ABC và đồng dạng suy ra Ac2 = CH x BC c)chứng minh hai tam giác ABD và tam giác CDB đồng dạng b chứng minh IH x BC = IA. AD
Cho tam giác ABC vuông tại A, có AB/BC 4/5, AC 18 cm. Vẽ đường phân giác BD của tam giác ABC. Trên cạnh AB lấy điểm H sao cho AH/AB 1/3, từ B vẽ đường thẳng vuông góc với đường thẳng HC tại E, đường thẳng BE cắt đường thẳng AC tại F. Biết AD 8 cm, DC 10cm và tam giác HAY đồng dạng tam giác HEB.a/ CM: AF.AC 1/3 AB^2b/ Trên Tia đối của tia FA lấy điểm M sao cho FM 2FA. CM: MB vuông góc BC( MỌI NGƯỜI GIÚP EM VỚI EM NỘP BÀI GẤP)
Đọc tiếp
Cho tam giác ABC vuông tại A, có AB/BC = 4/5, AC = 18 cm. Vẽ đường phân giác BD của tam giác ABC. Trên cạnh AB lấy điểm H sao cho AH/AB = 1/3, từ B vẽ đường thẳng vuông góc với đường thẳng HC tại E, đường thẳng BE cắt đường thẳng AC tại F. Biết AD = 8 cm, DC = 10cm và tam giác HAY đồng dạng tam giác HEB.
a/ CM: AF.AC = 1/3 AB^2
b/ Trên Tia đối của tia FA lấy điểm M sao cho FM = 2FA. CM: MB vuông góc BC
( MỌI NGƯỜI GIÚP EM VỚI EM NỘP BÀI GẤP)
Cho tam giác ABC vuông tại A (AB<AC),đường cao AH (H thuộc BC).
a) Chứng minh: tam giác HBA đồng dạng tam giác ABC
b) Chứng minh: AB2=BC.HB
c) gọi BD là phân giác của ABC (D thuộc BC) sao cho AD= 3cm Dc= 5 cm. TÍnh độ dài các đoạn thẳng AB, BC
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: ΔHBA đồng dạng với ΔABC
=>BH/BA=BA/BC
=>BA^2=BH*BC
Đúng 0
Bình luận (0)