Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 25cm, HC = 64cm. Tính góc B , C
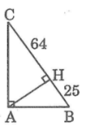
1. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB= 25cm, HC= 64cm. Tính AH, AC, góc B và góc C
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=40cm\\AC=8\sqrt{89}cm\end{matrix}\right.\)
Xét ΔACH vuông tại H có
\(\sin\widehat{C}=\dfrac{AH}{AC}=\dfrac{5}{\sqrt{89}}\)
\(\Leftrightarrow\widehat{C}\simeq32^0\)
hay \(\widehat{B}=58^0\)
Tam giác ABC vuông ở A, đường cao AH. Biết HB = 25cm, HC = 64cm. Tính góc B và góc C.
Tam giác ABC vuông ở A, ta có:
AH2 = 25.64 = 1600, suy ra AH = 40 (cm).
\(tgB=\frac{AH}{BH}=\frac{40}{25}=1,6\)
=> \(\widehat{B}\approx58^0\); \(\widehat{C}=32^0\).
hình đây nha
Ta có : AH^2 = CH . HB
=>AH=40
Ta lại có:tan B = AH / HB=40/25=1.6
=>B = 580
=>C = 320
Ta có : AH^2 = CH . HB
=>AH=40
Ta lại có:tan B = AH / HB=40/25=1.6
=>B = 580
=>C = 320
hc tốt
Cho tam giácABC vuông tại A, đường cao AH. Cho HB = 25cm, HC = 64cm. a) Tính chu vi và diện tích tam giác ABC b) Tính góc B, góc C c) Kẻ HM vuông góc AB, HN vuông góc AC. Tính MN
a: BC=25+64=89cm
AH=căn 25*64=40cm
S ABC=1/2*40*89=1780cm2
AB=căn 25*89=5căn 89cm
AC=căn 64*89=8 căn 89
=>C=13căn 89+89(cm)
b: tan B=AC/AB=8/5
=>góc B=58 độ
=>góc C=32 độ
c:
góc AMH=góc ANH=góc MAN=90 độ nên AMHN là hcn
=>MN=AH=40cm
Bài 1: Cho tam giác ABC vuông tại A giải Tam giác ABC biết: a) Góc B= 35 độ, BC=40 cm
b) AB=70cm, AC=60cm
c) AB=6cm, góc B=60 độ
d) AB=5cm, AC=7cm
2) Cho tam giác ABC góc A =90 độ đường cao AH biết HB=25cm, HC =64cm tín số đo góc B và C
3)Tam giác ABC có góc A =90 độ, AB=21cm, ggos C =40 độ tính độ dài đường phân giác BD
4) Tam giác ABC có góc B=70 độ góc C=35 độ đường cao AH=5cm tính độ dài AB,AC,B
Tam giác ABC vuông tại A ; đường cao AH; biết HB = 25cm; HC = 64 cm. Tính góc B
A. 42 °
B. 32 °
C. 58 o
D. 51 o
Đáp án C
Ta có: BC = HB + HC = 25 + 64 = 89 cm
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
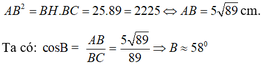
Cho tam giác ABC có góc A = 90 độ , đường cao AH
Biết BH = 25cm , HC = 64cm . Tính góc B , góc C
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH^2=HB\cdot HC\)
hay AH=40(cm)
Xét ΔABH vuông tại H có
\(\tan\widehat{B}=\dfrac{AH}{HB}=\dfrac{40}{25}=\dfrac{8}{5}\)
\(\Leftrightarrow\widehat{B}\simeq58^0\)
hay \(\widehat{C}=32^0\)
Cho tam giác ABC vuông tại A, kẻ đường cao AH
a)Biết HB=50cm, HC= 8cm. Tính chu vi tam giác ABC
b)Biết AC=12cm, HC=6cm. Tính AH, AB
c)Biết AH=12cm, BC=25cm. Tính AB+AC
Em xin cảm ơn ạ❤
a) \(AH^2=HB.HC=50.8=400\)
\(\Rightarrow AH=20\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.20\left(50+8\right)=\dfrac{1}{2}.20.58\left(cm^2\right)\)
mà \(S_{ABC}=\dfrac{1}{2}AB.AC\)
\(\Rightarrow AB.AC=20.58=1160\)
Theo Pitago cho tam giác vuông ABC :
\(AB^2+AC^2=BC^2\)
\(\Rightarrow\left(AB+AC\right)^2-2AB.AC=BC^2\)
\(\Rightarrow\left(AB+AC\right)^2=BC^2+2AB.AC\)
\(\Rightarrow\left(AB+AC\right)^2=58^2+2.1160=5684\)
\(\Rightarrow AB+AC=\sqrt[]{5684}=2\sqrt[]{1421}\left(cm\right)\)
Chu vi Δ ABC :
\(AB+AC+BC=2\sqrt[]{1421}+58=2\left(\sqrt[]{1421}+29\right)\left(cm\right)\)
Cho tam giác ABC vuông tại A có đường cao AH a/ cm AC2=HC.BC b/ biết HB=25cm, HC=36cm, tính BC, AH, AB
a: Xét ΔABC vuông tại A có AH là đường cao
nên AC^2=CH*CB
b: \(BC=25+36=61\left(cm\right)\)
\(AB=\sqrt{25\cdot61}=5\sqrt{61}\left(cm\right)\)
=>A\(C=6\sqrt{61}\left(cm\right)\)
Bài 1.Tam giác ABC vuông tại A, có AB = 21cm, \(\widehat{C}\) = 40°, phân giác BD của góc ABC, D ∈ AC. Tính
a) độ dài đoạn thẳng AC, BC
b) độ dài đoạn thẳng BD
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 25cm, HC = 64cm. Tính \(\widehat{B},\) \(\widehat{C}\)
Bài 3. Cho tam giác ABC vuông tại A có \(\widehat{B}\) = 30 °, AB = 6cm
a) Giải tam giác vuông ABC
b) Vẽ đường cao AH và trung tuyến Am của tam giác ABC. Tính diện tích tam giác AHM
Bài 2:
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)
\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)
\(AH^2=25.64\)
\(AH=\sqrt{1600}=40cm\)
Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)
\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)
\(\Rightarrow\widehat{B}\approx58^o\)
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)
\(58^o+\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}\approx90^o-58^o\)
\(\widehat{C}\approx32^o\)