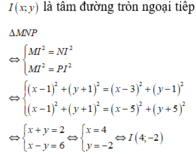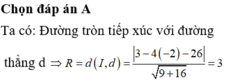Trong mặt phẳng tọa độ Oxy, cho đường tròn tâm I(1;-3), bán kính 2. Viết phương trình ảnh của đường tròn (I;2) qua phép đồng dạng có đưuọc từ việc thực hiện liên tiếp phép vị tự tâm O tỉ số 3 và phép đối xứng qua trục Ox.
PB
Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, đường tròn tâm I(3;-1) và bán kính R2 có phương trình là: A.
(
x
+
3
)
2
+
(
y
-
1
)
2
4
B.
(...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, đường tròn tâm I(3;-1) và bán kính R=2 có phương trình là:
A. ( x + 3 ) 2 + ( y - 1 ) 2 = 4
B. ( x - 3 ) 2 + ( y - 1 ) 2 = 4
C. ( x - 3 ) 2 + ( y + 1 ) 2 = 4
D. ( x + 3 ) 2 + ( y + 1 ) 2 = 4
Trong mặt phẳng tọa độ Oxy, đường tròn tâm I(3;-1) và bán kính R2 có phương trình là:
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, đường tròn tâm I(3;-1) và bán kính R=2 có phương trình là:
![]()
![]()
![]()
![]()
Trong mặt phẳng Oxy cho tam giác MNP với
M
1
;
-
1
,
N
3
;
1
,
P
5
;
-
5
;. Tọa độ tâm I đường tròn ngoại tiếp tam giác MNP là: A.
I
4
;
2
B.
I...
Đọc tiếp
Trong mặt phẳng Oxy cho tam giác MNP với M 1 ; - 1 , N 3 ; 1 , P 5 ; - 5 ;. Tọa độ tâm I đường tròn ngoại tiếp tam giác MNP là:
A. I 4 ; 2
B. I - 4 ; 2
C. I 4 ; - 4
D. I 4 ; - 2
Trong mặt phẳng tọa độ Oxy cho đường tròn tâm I(2;-2), bán kính R 4. Viết phương trình đường tròn là ảnh của đường tròn (I;R) qua phép vị tự tâm O, tỉ số
1
2
. A.
x
-
4
2
+
(
y
+
4
)
2
4
B. ...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho đường tròn tâm I(2;-2), bán kính R = 4. Viết phương trình đường tròn là ảnh của đường tròn (I;R) qua phép vị tự tâm O, tỉ số 1 2 .
A. x - 4 2 + ( y + 4 ) 2 = 4
B. x - 4 2 + ( y + 4 ) 2 = 64
C. x - 1 2 + ( y + 1 ) 2 = 4
D. x - 1 2 + ( y + 1 ) 2 = 64
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có
A
−
4
;
1
,
B
2
;
4
,
C(2; -2). Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác đã cho. A.
I
1
4
;
1
.
B. ...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A − 4 ; 1 , B 2 ; 4 , C(2; -2). Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác đã cho.
A. I 1 4 ; 1 .
B. I - 1 4 ; 1 .
C. I 1 ; 1 4 .
D. I 1 ; - 1 4 .
Gọi I( x; y). Ta có A I → = x + 4 ; y − 1 B I → = x − 2 ; y − 4 C I → = x − 2 ; y + 2 .
Do I là tâm đường tròn ngoại tiếp tam giác ABC nên I A = I B = I C ⇔ I A 2 = I B 2 I B 2 = I C 2
⇔ x + 4 2 + y − 1 2 = x − 2 2 + y − 4 2 x − 2 2 + y − 4 2 = x − 2 2 + y + 2 2 ⇔ x + 4 2 + y − 1 2 = x − 2 2 + y − 4 2 y − 4 2 = y + 2 2 ⇔ x + 4 2 = x − 2 2 + ( 1 − 4 ) 2 y = 1 ⇔ x 2 + 8 x + 16 = x 2 − 4 x + 4 + 9 y = 1 ⇔ x = − 1 4 y = 1 .
Chọn B.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, tính bán kính đường tròn tâm I(1;-2) và tiếp xúc với đường thẳng d: 3x-4y-26=0
A. R = 3
B. R = 5
C. R = 9.
D. R = 3 5
Trong mặt phẳng tọa độ Oxy, cho đường tròn (S) có tâm I nằm trên đường thẳng
y
-
x
, bán kính bằng
R
3
và tiếp xúc với các trục tọa độ. Lập phương trình của (S), biết hoành độ tâm I là số dương. A.
x
-
3
2
+
y
-
3...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn (S) có tâm I nằm trên đường thẳng y = - x , bán kính bằng R = 3 và tiếp xúc với các trục tọa độ. Lập phương trình của (S), biết hoành độ tâm I là số dương.
A. x - 3 2 + y - 3 2 = 9
B. x - 3 2 + y + 3 2 = 9
C. x - 3 2 - y - 3 2 = 9
D. x + 3 2 + y + 3 2 = 9
Gọi I a ; - a a > 0 thuộc đường thẳng y = - x
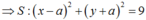
(S) tiếp xúc với các trục tọa độ
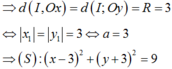
Chọn B.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(- 4;1); B(2; 4); C(2; -2). Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác đã cho. A.
I
1
4
;
1
.
B.
I
−
1
4
;
1
.
C.
I
1...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(- 4;1); B(2; 4); C(2; -2). Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác đã cho.
A. I 1 4 ; 1 .
B. I − 1 4 ; 1 .
C. I 1 ; 1 4 .
D. I 1 ; − 1 4 .
Gọi I(x, y). Ta có A I → = x + 4 ; y − 1 B I → = x − 2 ; y − 4 C I → = x − 2 ; y + 2 .
Do I là tâm đường tròn ngoại tiếp tam giác ABC nên:
I A = I B = I C ⇔ I A 2 = I B 2 I B 2 = I C 2
⇔ x + 4 2 + y − 1 2 = x − 2 2 + y − 4 2 x − 2 2 + y − 4 2 = x − 2 2 + y + 2 2 ⇔ x + 4 2 = x − 2 2 + 9 y = 1 ⇔ x = − 1 4 y = 1 .
Chọn B.
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho A(-2;2),B(6;6),C(2;-2).
a) Tìm tọa độ trực tâm H của tam giác ABC; tọa độ tâm đường tròn ngoại tiếp I tam giác ABC; tọa độ trọng tâm G của tam giác ABC.
b) Chứng minh : IH=-3IG.
c) Gọi AD là đường kính của đường tròn ngoại tiếp tam giác ABC. Chứng minh tứ giác ABCD là hình bình hành.
mong mn giúp mình với ạ
Trong mặt phẳng tọa độ Oxy, đường tròn (C) tâm I(-3;4), bán kính R 6 có phương trình là: A. (x + 3
)
2
+ (y - 4
)
2
36 B. (x - 3
)
2
+ (y + 4
)
2
6 C. (x + 3
)
2
+ (y - 4
)
2
6 D. (x - 3
)
2...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, đường tròn (C) tâm I(-3;4), bán kính R = 6 có phương trình là:
A. (x + 3 ) 2 + (y - 4 ) 2 = 36
B. (x - 3 ) 2 + (y + 4 ) 2 = 6
C. (x + 3 ) 2 + (y - 4 ) 2 = 6
D. (x - 3 ) 2 + (y + 4 ) 2 = 36
Chọn A.
Phương trình đường tròn (C) tâm I(-3;4), bán kính R = 6 là:
[x - (-3) ] 2 + (y - 4 ) 2 = 6 2 ⇒ (x + 3 ) 2 + (y - 4 ) 2 = 36
Đúng 0
Bình luận (0)