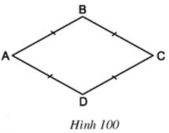
Chứng minh rằng tứ giác ABCD trên hình 100 cũng là một hình bình hành.
PB
Những câu hỏi liên quan
Cho hình bình hành ABCD, Trên cạnh AB lấy điểm M, trên cạnh CD lấy điểm N sao cho a, Chứng minh rằng: . b, Chứng minh tứ giác AMCN là hình bình hành. c, Chứng minh tứ giác BMDN là hình bình hành
Đọc tiếp
Cho hình bình hành ABCD, Trên cạnh AB lấy điểm M, trên cạnh CD lấy điểm N sao cho 
a, Chứng minh rằng: 
.
b, Chứng minh tứ giác AMCN là hình bình hành.
c, Chứng minh tứ giác BMDN là hình bình hành
Cho hình bình hành ABCD . Tứ giác A,H hạ AH ,AK lâng lượt vuông góc với BD .chứng minh rằng tues giác AHCK cũng là hình bình hành
Sửa đề: Từ A,C hạ AH,CK lần lượt vuông góc với BD
Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔAHD=ΔCKB
=>AH=CK
AH\(\perp\)BD
CK\(\perp\)BD
Do đó: AH//CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD . Trên cạnh AB lấy điểm E , trên cạnh CD lấy điểm F sao cho AE = CF. a / Chứng minh DE = BF b / Chứng minh tứ giác AECF là hình bình hành . c / Chứng minh tứ giác BEDF là hình bình hành
a: Ta có: AE+EB=AB
DF+FC=DC
mà AE=FC
và AB=DC
nên EB=DF
Xét tứ giác EBFD có
EB//DF
EB=DF
Do đó: EBFD là hình bình hành
Suy ra: DE=BF
b: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Đúng 1
Bình luận (0)
Chứng minh rằng hình chữ nhật ABCD trên hình 84 cũng là một hình bình hành, một hình thang cân.
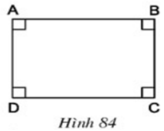
- ABCD có các góc đối bằng nhau (đều là góc vuông) nên ABCD là hình bình hành
- ABCD là hình thang (vì AB // CD),
hai góc ở đáy: góc D = góc C ⇒ ABCD là hình thang cân
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có M, N là trung điểm AB, CD . Gọi P, Q nằm trên cạnh AD, BC
tương ứng sao cho AP=CQ. a. Chứng minh rằng ∆𝑀𝐴𝑃 = ∆𝑁𝐶𝑄. b. Chứng minh rằng ∆𝑀𝐵𝑄 = ∆𝑁𝐷𝑃. c. Chứng minh rằng tứ giác MPNQ là hình bình hành. d. Chứng minh rằng ba đường thẳng MN, PQ, BD đồng quy tại một điể
a: Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(CN=ND=\dfrac{CD}{2}\)
mà AB=CD
nên AM=MB=CN=ND
Xét ΔMAP và ΔNCQ có
MA=CN
\(\widehat{A}=\widehat{C}\)
AP=CQ
Do đó: ΔMAP=ΔNCQ
b: Ta có: BQ+CQ=BC
AP+DP=AD
mà BC=AD
và CQ=AP
nên BQ=DP
Xét ΔMBQ và ΔNDP có
MB=ND
\(\widehat{B}=\widehat{D}\)
BQ=DP
Do đó: ΔMBQ=ΔNDP
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD . Trên cạnh AB lấy điểm E , trên cạnh CD lấy điểm F sao
cho AE CF .Gọi O là giao điểm của AC và BD.
a) Chứng minh: tứ giác AECF là hình bình hành.
b) Chứng minh: tứ giác BEDF là hình bình hành.
c) Chứng minh E, O, F thẳng hàng.
Đọc tiếp
Cho hình bình hành ABCD . Trên cạnh AB lấy điểm E , trên cạnh CD lấy điểm F sao
cho AE= CF .Gọi O là giao điểm của AC và BD.
a) Chứng minh: tứ giác AECF là hình bình hành.
b) Chứng minh: tứ giác BEDF là hình bình hành.
c) Chứng minh E, O, F thẳng hàng.
Cho hình bình hành ABCD. Các tia phân giác của các góc của hình bình hành cắt nhau tạo thành tứ giác EFGH.
a) Tứ giác EFGH là hình gì ? Vì sao ?
b) Chứng minh rằng EG = FH và bằng hiệu giữa hai cạnh kề một đỉnh của hình bình hành ABCD.
c) Hình bình hành ABCD cần có thêm điều kiện gì để EFGH là hình vuông?
H24
SGK Toán 8 tập 1– Chân trời sáng tạo
21 tháng 7 2023 lúc 22:35
Cho hình bình hành \(ABCD\). Gọi \(E\) là trung điểm của \(AD\), \(F\) là trung điểm của \(BC\)
a) Chứng minh rằng tứ giác \(EBFD\) là hình bình hành
b) Gọi \(O\) là giao điểm của hai đường chéo của hình bình hành \(ABCD\). Chứng minh rằng ba điểm \(E\), \(O\), \(F\) thẳng hàng.
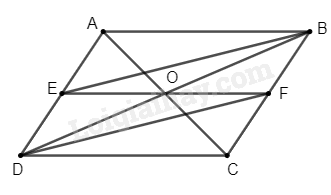
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AD = BC\); \(AD\) // \(BC\)
Mà \(E\), \(F\) là trung điểm của \(AD\), \(BC\) (gt)
Suy ra \(AE = ED = BF = FC\)
Xét tứ giác \(EBFD\) ta có:
\(ED = FB\) (cmt)
\(ED\) // \(BF\) (do \(AD\) // \(BC\))
Suy ra \(EDFB\) là hình bình hành
b) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\)
Mà \(DEBF\) là hình bình hành (gt)
Suy ra \(O\) cũng là trung điểm của \(EF\)
Suy ra \(E\), \(O\), \(F\) thẳng hàng
Đúng 1
Bình luận (0)
Trên mặt phẳng (α) cho hình bình hành
A
1
B
1
C
1
D
1
. Về một phía đối với mặt phẳng (α) ta dựng hình bình hành
A
2
B
2
C
2
D
2
. Trên các đoạn
A
1
A...
Đọc tiếp
Trên mặt phẳng (α) cho hình bình hành A 1 B 1 C 1 D 1 . Về một phía đối với mặt phẳng (α) ta dựng hình bình hành A 2 B 2 C 2 D 2 . Trên các đoạn A 1 A 2 , B 1 B 2 , C 1 C 2 , D 1 D 2 ta lần lượt lấy các điểm A, B, C, D sao cho
A A 1 A A 2 = B B 1 B B 2 = C C 1 C C 2 = D D 1 D D 2 = 3
Chứng minh rằng tứ giác ABCD là hình bình hành
