Dựng hình thang cân ABCD, biết đáy CD = 3cm, đường chéo AC = 4cm, góc ∠D = 80o.
PB
Những câu hỏi liên quan
Dựng hình thang cân ABCD, biết đáy CD = 3cm, đường chéo AC = 4cm, góc ∠D = 80o.
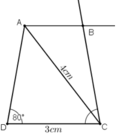
a) Phân tích
Giả sử dựng được hình thang ABCD theo yêu cầu đề bài.
Ta dựng được đoạn thẳng CD = 3cm.
Điểm A phải thỏa mãn hai điều kiện:
+ Tia DA tạo với DC một góc bằng 80º.
+ CA = 4cm nên A thuộc cung tròn tâm C bán kính 4cm.
ABCD là hình thang nên AB // CD
Hình thang ABCD cân nên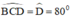 
Vì vậy điểm B phải thỏa mãn 2 điều kiện:
+ B nằm trên đường thẳng đi qua A và song song với CD
+ Tia CB tạo với CD một góc 80º.
b) Cách dựng
+ Dựng đoạn CD = 3cm.
+ Dựng tia Dx thỏa mãn
+ Dựng cung tròn tâm C, bán kí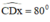
nh 4cm cắt tia Dx tại A.
+ Qua A dựng đường thẳng m song song với CD.
+ Dựng tia Cy trên cùng nửa mặt phẳng chứa điểm A, bờ CD thỏa mãn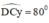 
+ Tia Cy cắt đường thẳng m tại B.
Ta dựng được hình thang ABCD
c) Chứng minh
+ Tứ giác ABCD là hình thang vì AB // CD
+ Hình thang ABCD có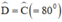 
nên là hình thang cân.
+ Hình thang cân ABCD có CD = 3cm, AC = 4cm,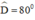 
nên thỏa mãn yêu cầu đề bài.
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện đề bài.
Đúng 0
Bình luận (0)
Dựng hình thang cân ABCD, biết đáy CD = 3cm, đường chéo AC = 4cm,D^=80
1. Dựng hình thang cân ABCD (AB//CD) biết AB=1cm, CD=3cm và AD=2cm
2. Dựng hình thang cân ABCD, biết đáy CD=4cm, cạnh bên AD=2cm, đường chéo BD=3cm
1. Dựng hình thang cân ABCD (AB//CD) biết AB1cm, CD3cm và AD2cm2. Dựng hình thang cân ABCD, biết đáy CD4cm, cạnh bên AD2cm, đường chéo BD3cm
Đọc tiếp
1. Dựng hình thang cân ABCD (AB//CD) biết AB=1cm, CD=3cm và AD=2cm
2. Dựng hình thang cân ABCD, biết đáy CD=4cm, cạnh bên AD=2cm, đường chéo BD=3cm
Dựng hình thang cân ABCD, biết đáy CD = 3cm, đường chéo AC = 4cm, \(\widehat{D}=80^0\) ?
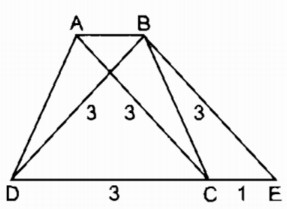
Dựng hình thang cân ABCD, biết hai đáy AB = lcm, CD = 3cm, đường chéo BD = 3cm.
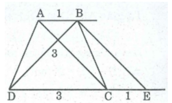
Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán
Từ B kẻ đường thẳng song song với AC cắt CD tại E. Tứ giác ABEC là hình thang có hai cạnh bên song song nên CE = AB = l cm, BE = AC = 3cm
Tam giác BDE xác định được, ta cần xác định đỉnh C và A.
- Đỉnh C nằm trên tia DE cách D một khoảng bằng 3cm
- Đỉnh A nằm trên đường thẳng đi qua B và song song với CD, A cách C một khoảng bằng 3 cm. (ABCD là hình thang cân nên AC = BD = 3 cm)
Cách dựng:
- Dựng ∆ BDE biết BD = 3cm, BE = 3cm , DE = 4cm
- Dựng điểm C trên tia DE sao cho DC = 3cm
- Dựng đường thẳng d đi qua B song song với CD.
- Dựng cung tròn tâm C bán kính 3 cm cắt đường thắng d tại A. Nối AD ta có hình thang ABCD dựng được.
Chứng minh: Thật vậy theo cách dựng ta có AB // CD.
Tứ giác ABCD là hình thang. CD = 3cm, AC = BD = 3cm. Vậy ABCD là hình thang cân thỏa mãn điều kiện bài toán.
Bài toán có một nghiệm hình.
Đúng 0
Bình luận (0)
Dựng hình thang cân ABCD, biết hai đáy AB = 1cm, CD = 3cm, đường chéo BD = 3cm
dựng hình thang cân ABCD, biết hai đáy AB = 1cm,CD =3cm , đường chéo BD = 3cm
Dựng hình thang ABCD (AB // CD), biết ba cạnh: AD = 2cm, CD = 4cm, BC = 3cm và đường chéo AC = 5cm.
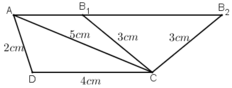
* Dựng hình:
- Dựng tam giác ADC có AD = 2cm, DC = 4cm, CA = 5cm.
- Dựng tia Ax song song với CD.
- Đường tròn (C; 3cm) cắt Ax tại B1 và B2.
Hình thang ABCD với B ≡ B1 hoặc B ≡ B2 là hình thang cần dựng.
* Chứng minh
+ Tứ giác ABCD có AD = 2cm, DC = 4cm, CA = 5cm.
+ Ax // CD ⇒ AB // CD ⇒ ABCD là hình thang.
+ B ∈ (C; 3cm) ⇒ BC = 3cm.
Đúng 0
Bình luận (0)