Trong không gian cho ba vecto tùy ý a → , b → , c →
Gọi u → = a → − 2 b → , v → = 3 b → − c → , w → = 2 c → − 3 a →
Chứng tỏ rằng ba vecto u → , v → , w → đồng phẳng.
Trong không gian Oxyz cho một vecto a → tùy ý khác vecto 0 → . Gọi α , β , γ là ba góc tạo bởi ba vecto đơn vị i → , j → , k → trên ba trục Ox, Oy, Oz và vecto a → . Chứng minh rằng: cos 2 α + cos 2 β + cos 2 γ = 1
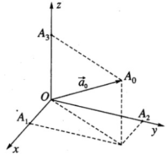
Gọi a 0 → là vecto đơn vị cùng hướng với vecto a →
ta có 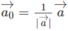
Gọi O A 0 → = a 0 → và các điểm A 1 , A 2 , A 3 theo thứ tự là hình chiếu vuông góc của điểm A 0 trên các trục Ox, Oy, Oz.
Khi đó ta có:
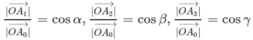
Vì
![]()
![]()
Ta có:
![]()
ta suy ra:
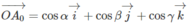
hay
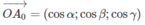
Vì O A 0 → = a 0 → mà | a 0 → | = 1 nên ta có: cos 2 α + cos 2 β + cos 2 γ = 1
Cho ba vecto a → , b → , c → trong không gian. Chứng minh rằng nếu m a → + n b → + p c → = 0 → và một trong ba số m, n, p khác không thì ba vecto a → , b → , c → đồng phẳng
Giả sử p ≠ 0 ta có:
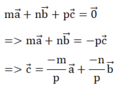
Do đó, ba vecto a → , b → , c → đồng phẳng theo định lí 1
Trong không gian cho ba vectơ tùy ý \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\)
Gọi \(\overrightarrow{u}=\overrightarrow{a}-2\overrightarrow{b};\overrightarrow{v}=3\overrightarrow{b}-\overrightarrow{c};\overrightarrow{w}=2\overrightarrow{c}-3\overrightarrow{a}\)
Chứng tỏ rằng ba vectơ \(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\) đồng phẳng ?
Trong không gian Oxyz, cho các vecto a → = ( m ; 1 ; 0 ) , b → = ( 2 ; m - 1 ; 1 ) , c → = ( 1 ; m + 1 ; 1 ) . Tìm m để ba vecto a → , b → , c → đồng phẳng
A. m= - 2
B. m = 3 2
C. m = - 1
D. m = - 1 2
Trong không gian Oxy cho ba vecto a ⇀ = 2 ; - 5 ; 3 ; b ⇀ = 0 ; 2 ; - 1 ; c ⇀ = 1 ; 7 ; 2 . Tọa độ của vecto u ⇀ = 4 a ⇀ - b ⇀ 3 + 3 c ⇀ , là:
A. u ⇀ = 11 ; 1 3 ; 55 3
B. u ⇀ = - 11 ; 1 3 ; 55 3
C. u ⇀ = 11 ; - 1 3 ; 55 3
D. u ⇀ = 11 ; - 1 3 ; - 55 3
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A ( 1;1;1) B(2,1,0) C(2,0,2). Gọi P là mp chứa BC và cách A một khoảng lớn nhất. Tìm vecto pháp tuyến của (P)
kẻ \(AH\perp BCtạiH\)
\(\overrightarrow{CB}=\left(0;1;-2\right)\)
\(\Rightarrow p+BC:\left\{{}\begin{matrix}x=1\\y=t\\y=2-2t\end{matrix}\right.\\ \Rightarrow H\left(2;t;2-2t\right)\)
\(\Rightarrow\overrightarrow{AH}=\left(1;t-1;1-2t\right)\perp\overrightarrow{CB}\)
\(\Rightarrow0.1+1\left(t-1\right)-2\left(1-2t\right)=0\)
\(\Leftrightarrow t=\dfrac{3}{5}\Rightarrow\overrightarrow{AH}=\left(1;-\dfrac{2}{3};-\dfrac{1}{5}\right)\)
Vì AK≤AH∀(p)
\(\Rightarrow AK_{\max\limits}=AH\Leftrightarrow K\equiv H\)
\(\Rightarrow\overrightarrow{AH}\perp\left(P\right)\Rightarrow\overrightarrow{AH}là1vtpt\)
Trong không gian Oxyz, cho bốn điểm A (3;1;0), B(2;0;-1), C(0;2;-1), D (0;0;2). Với mỗi điểm M tùy ý, đặt T=MA+MB+MC+MD. Gọi M ∘ a ; b ; c sao cho T đạt giá trị nhỏ nhất. Lúc đó, tổng a + 5 b + c bằng
A. 3.
B. -13.
C. 7.
D. 4
Trong không gian tọa độ O ; i → , j → , k → , cho ba vecto a → = 1 ; 2 ; 3 , b → = - 2 ; 0 ; 1 , c → = - 1 ; 0 ; 1 . Tìm tọa độ của vecto n → = a → + b → + 2 c → - 3 i →
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là các số thực dương thay đổi tùy ý sao cho a 2 + b 2 + c 2 = 3 . Khoảng cách từ O đến mặt phẳng (ABC) lớn nhất bằng
A. 1 3
B. 3
C. 1 3
D. 1
Đáp án C
Vì OA, OB, OC đôi một vuông góc với nhau 1 d 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
Với d là khoảng cách từ O -> (ABC) suy ra 1 d 2 = 1 a 2 + 1 b 2 + 1 c 2
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức, ta có x 2 a + y 2 b + z 2 c ≥ x + y + z 2 a + b + c
Vậy d m a x = 1 3