Lập bảng biến thiên và vẽ đồ thị của các hàm số: y = 3x2 - 4x + 1
PB
Những câu hỏi liên quan
Lập bảng biến thiên và vẽ đồ thị của các hàm số: y = -3x2 + 2x - 1
y = –3x2 + 2x – 1.
+ Tập xác định: R
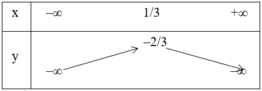
+ Đỉnh A(1/3 ; –2/3).
+ Trục đối xứng x = 1/3.
+ Đồ thị không giao với trục hoành.
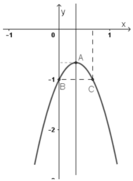
+ Giao điểm với trục tung là B(0; –1).
Điểm đối xứng với B(0 ; –1) qua đường thẳng x = 1/3 là C(2/3 ; –1).
+ Bảng biến thiên:
+ Đồ thị hàm số :
Đúng 0
Bình luận (0)
Lập bảng biến thiên và vẽ đồ thị của các hàm số: y = 4x2 - 4x + 1
y = 4x2 – 4x + 1.
+ Tập xác định : R
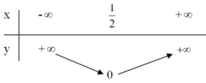
+ Đỉnh A(1/2; 0).
+ Trục đối xứng x = 1/2.
+ Giao điểm với trục hoành tại đỉnh A.
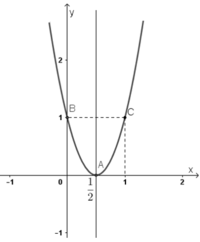
+ Giao điểm với trục tung B(0; 1).
Điểm đối xứng với B(0;1) qua đường thẳng x = 1/2 là C(1; 1).
+ Bảng biến thiên:
+ Đồ thị hàm số:
Đúng 0
Bình luận (0)
Lập bảng biến thiên và vẽ đồ thị của hàm số bậc hai
y = 3 x 2 + 2 3 x + 2
Bảng biến thiên
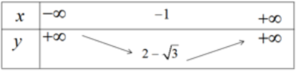
Hàm số nghịch biến trên khoảng ( - ∞ ; - 1 ) đồng biến trên khoảng ( - 1 ; + ∞ )
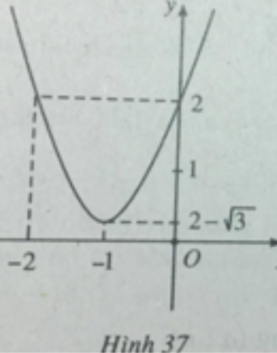
Đỉnh parabol ( - 1 ; 2 - 3 )
Đồ thị hàm số được vẽ trên hình 37.
Đúng 0
Bình luận (0)
Lập bảng biến thiên và vẽ đồ thị của hàm số bậc hai
y = - 3 x 2 - 6 x + 4
Bảng biến thiên
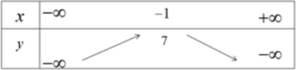
Hàm số đồng biến trên khoảng (-∞; -1) nghịch biến trên khoảng (-1; +∞)
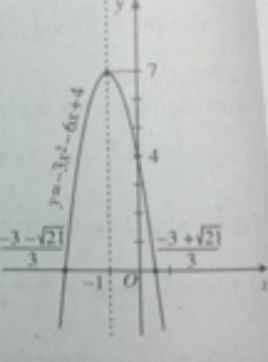
Đỉnh parabol I(-1;7). Đồ thị của hàm số y = - 3 x 2 - 6 x + 4 được vẽ trên hình 36.
Đúng 0
Bình luận (0)
Lập bảng biến thiên và vẽ đồ thị của các hàm số: y = -x2 + 4x - 4
y = –x2 + 4x – 4.
+ Tập xác định: R
+ Đỉnh: I (2; 0)
+ Trục đối xứng: x = 2.
+ Giao điểm với trục hoành: A(2; 0).
+ Giao điểm với trục tung: B(0; –4).
Điểm đối xứng với điểm B(0; –4) qua đường thẳng x = 2 là C(4; –4).
+ Bảng biến thiên:
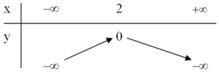
+ Đồ thị hàm số:
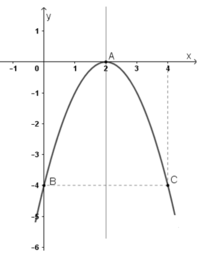
Đúng 0
Bình luận (0)
Lập bảng biến thiên và vẽ đồ thị của hàm số bậc hai
y = 2 x 2 + 4 x - 6
Hàm số bậc hai đã cho có a = 2; b = 4; c = -6;
![]()
Vì a > 0, ta có bảng biến thiên
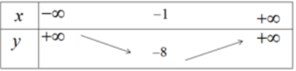
Hàm số nghịch biến trên khoảng (-∞; -1) đồng biến trên khoảng (-1; +∞)
Để vẽ đồ thị ta có trục đối xứng là đường thẳng x = -1; đỉnh I(-1;-8); giao với tục tung tại điểm (0;-6); giao với trục hoành tại các điểm (-3;0) và (1;0).
Đồ thị của hàm số y = 2 x 2 + 4 x - 6 được vẽ trên hình 35.
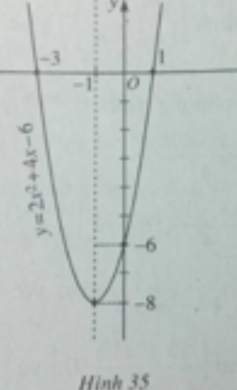
Đúng 0
Bình luận (0)
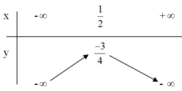
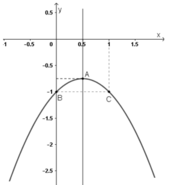
Lập bảng biến thiên và vẽ đồ thị của các hàm số: y = -x2 + x - 1
y = –x2 + x – 1
+ Tập xác định R
+ Đỉnh A(1/2 ; –3/4).
+ Trục đối xứng x = 1/2.
+ Đồ thị không giao với trục hoành.
+ Giao điểm với trục tung: B(0; –1).
Điểm đối xứng với B(0 ; –1) qua đường thẳng x = 1/2 là C(1 ; –1).
+ Bảng biến thiên:
+ Đồ thị hàm số :
Đúng 0
Bình luận (0)
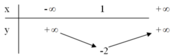
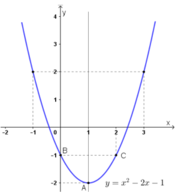
Lập bảng biến thiên và vẽ đồ thị của các hàm số: y = x2 - 2x - 1
Hàm số y = x2 – 2x – 1 có a = 1 > 0 ; b = –2 ; c = –1:
+ Tập xác định D = R.
+ Nghịch biến trên (–∞ ; 1) ; đồng biến trên (1 ; + ∞).
Bảng biến thiên:
+ Đồ thị hàm số là parabol có:
Đỉnh A(1 ; –2)
Trục đối xứng là đường thẳng x = 1.
Giao điểm với Oy tại B(0 ; –1). Điểm đối xứng với B qua đường thẳng x = 1 là C(2 ; –1).
Đi qua các điểm (3 ; 2) và (–1 ; 2).
Đúng 0
Bình luận (0)
Lập bảng biến thiên và vẽ đồ thị của các hàm số: y = 2x2 + x + 1
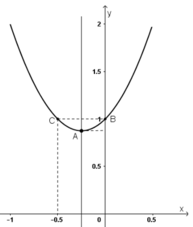
y = 2x2 + x + 1
+ Tập xác định: R
+ Đỉnh A(–1/4 ; 7/8).
+ Trục đối xứng x = –1/4.
+ Đồ thị không giao với trục hoành.
+ Giao điểm với trục tung B(0; 1).
Điểm đối xứng với B(0 ; 1) qua đường thẳng x = –1/4 là C(–1/2 ; 1)
+ Bảng biến thiên:
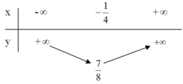
+ Đồ thị hàm số:
Đúng 0
Bình luận (0)

