Từ định nghĩa của sinα và cosα, hãy phát biểu ý nghĩa hình học của chúng.
PB
Những câu hỏi liên quan
Hãy nêu định nghĩa của sinα , cosα và giải thích vì sao ta có:
sin(α +k2 π)=sinα;k ∈Z
cos(α +k2 π)=cosα;k ∈Z
+) Định nghĩa của sin α; cos α
Trên đường tròn lượng giác, xét cung AM có số đo α
Gọi H và K lần lượt là hình chiếu của M trên trục Ox, Oy.
Tung độ y = OK¯ của điểm M được gọi là sin của α : sin α = OK¯
Hoành độ x = OH¯ của điểm M được gọi là cos của α : cos α = OH¯
Trên đường tròn lượng giác trong mặt phẳng Oxy, lấy điểm A (1; 0) làm gốc.
Khi đó các cung có số đo hơn kém nhau một bội của 2π có điểm cuối trùng nhau.
Giả sử cung α có điểm cuối là M(x; y)
Khi đó với mọi k ∈ Z thì cung α + k2π cũng có điểm cuối là M.
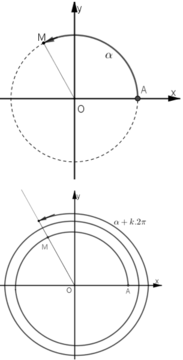
sin α = y, sin (α + k2π) = y nên sin(α + k2π) = sinα
cos α = x, cos(α + k2π) = x nên cos(α + k2π) = cosα
Đúng 0
Bình luận (0)
Từ định nghĩa của sinα, cosα. Hãy chứng minh hằng đẳng thức đầu tiên, từ đó suy ra các hằng đẳng thức còn lại.
cosα = OH¯; sinα = OK¯
Do tam giác OMK vuông tại K nên:
sin2 α + cos2 α = OK¯2 + OH¯2 = OK2 + MK2 = OM2 = 1.
Vậy sin2 α + cos2 α = 1.
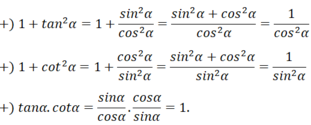
Đúng 0
Bình luận (0)
Không dùng bảng số và máy tính, hãy xác định dấu của sinα và cosα với
α = 210 o
Không dùng bảng số và máy tính, hãy xác định dấu của sinα và cosα với
α = 1280 o
sin 1280 ο = sin ( 3 . 360 ο + 120 ο ) = sin 200 ο < 0
cos 1280 ο = cos 200 ο < 0
Đúng 0
Bình luận (0)
Không dùng bảng số và máy tính, hãy xác định dấu của sinα và cosα với
α = 334 o
Không dùng bảng số và máy tính, hãy xác định dấu của sinα và cosα với
α = - 1876 o
sin ( - 1876 ο ) = sin ( - 1800 ο - 76 ο ) = sin ( - 76 ο ) = - sin 76 ο < 0
cos ( - 1876 ο ) = cos ( - 76 ) ο = cos 76 ο > 0
Đúng 0
Bình luận (0)
Không dùng bảng số và máy tính, hãy xác định dấu của sinα và cosα với
α = - 235 o
sin ( - 235 ο ) = sin ( - 180 ο - 55 ο ) = - sin ( - 55 ο ) = sin 55 ο > 0 , cos ( - 235 ο ) < 0
Đúng 0
Bình luận (0)
Không dùng bảng số và máy tính, hãy xác định dấu của sinα và cosα với
α = 135 o


