Cho hình bình hành ABCD. Chứng minh rằng: 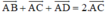
PB
Những câu hỏi liên quan
Hình dưới cho ABCD là hình bình hành. Chứng minh rằng: EGFH là hình bình hành.
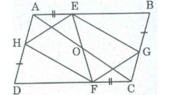
+) Ta có: AH + HD = AD
CG + GB = CB
Mà AD = CB ( vì ABCD là hình bình hành).
DH = GB ( giả thiết)
Suy ra: AH = CG.
Xét ∆ AEH và ∆ CFG:
AE = CF (gt)
∠ A = ∠ C (tính chất hình bình hành)
AH = CG ( chứng minh trên).
Do đó: ∆ AEH = ∆ CFG (c.g.c)
⇒ EH = FG
Xét ∆ BEG và ∆ DFH, ta có:
BG = DH (gt)
∠ B = ∠ D (tính chất hình bình hành)
BE = DF (vì AB = CD và AE = CF nên AB – AE = CD – CF hay BE = DF )
Do đó: ∆ BEG = ∆ DFH (c.g.c) ⇒ EG = FH
Suy ra: Tứ giác EGFH là hình bình hành (vì có các cặp cạnh đối bằng nhau)
Đúng 0
Bình luận (0)
Hình bên cho ABCD là hình bình hành. Chứng minh rằng AECF là hình bình hành.
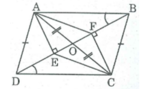
Gọi O là'giao điểm của AC và BD, ta có:
OA = OC (tính chất hình bình hành) (1)
Xét hai tam giác vuông AEO và CFO, ta có:
∠ (AEO) = ∠ (CFO) = 90 0
OA = OC (chứng minh trên)
∠ (AOE) = ∠ (COF) (đối đỉnh)
Do đó ∆ AEO = ∆ CFO (cạnh huyền, góc nhọn)
⇒ OE = OF (2)
Từ (1) và (2) suy ra tứ giác AECF là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD, Trên cạnh AB lấy điểm M, trên cạnh CD lấy điểm N sao cho a, Chứng minh rằng: . b, Chứng minh tứ giác AMCN là hình bình hành. c, Chứng minh tứ giác BMDN là hình bình hành
Đọc tiếp
Cho hình bình hành ABCD, Trên cạnh AB lấy điểm M, trên cạnh CD lấy điểm N sao cho ![]()
a, Chứng minh rằng: ![]() .
.
b, Chứng minh tứ giác AMCN là hình bình hành.
c, Chứng minh tứ giác BMDN là hình bình hành
trên hình 8 ,cho ABCD là hình bình hành .Chứng minh rằng AECF là hình bình hành
Cho hình bình hành \(ABCD\). Gọi \(E\) là trung điểm của \(AD\), \(F\) là trung điểm của \(BC\)
a) Chứng minh rằng tứ giác \(EBFD\) là hình bình hành
b) Gọi \(O\) là giao điểm của hai đường chéo của hình bình hành \(ABCD\). Chứng minh rằng ba điểm \(E\), \(O\), \(F\) thẳng hàng.
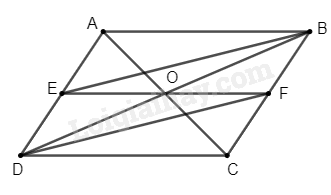
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AD = BC\); \(AD\) // \(BC\)
Mà \(E\), \(F\) là trung điểm của \(AD\), \(BC\) (gt)
Suy ra \(AE = ED = BF = FC\)
Xét tứ giác \(EBFD\) ta có:
\(ED = FB\) (cmt)
\(ED\) // \(BF\) (do \(AD\) // \(BC\))
Suy ra \(EDFB\) là hình bình hành
b) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\)
Mà \(DEBF\) là hình bình hành (gt)
Suy ra \(O\) cũng là trung điểm của \(EF\)
Suy ra \(E\), \(O\), \(F\) thẳng hàng
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD có AB=2BC. Gọi M và N là Trung điểm của AB, CD. a) chứng minh rằng AMND là hình thoi. b)chứng minh rằng MBND là hình bình hành. C) chứng minh rằng AC, BD, MN đồng quy
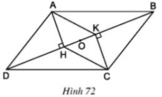
Cho hình 72. Trong đó ABCD là hình bình hành
a) Chứng minh rằng AHCK là hình bình hành
b) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng.
a)+ ABCD là hình bình hành
⇒ AD // BC và AD = BC.
⇒ ∠ADH = ∠CBK (Hai góc so le trong).
Hai tam giác vuông AHD và CKB có:
AD = BC
∠ADH = ∠CBK
⇒ ΔAHD = ΔCKB (cạnh huyền, góc nhọn)
⇒ AH = CK
+ AH ⊥ BD; CK ⊥ BD ⇒ AH // CK
Tứ giác AHCK có AH // CK, AH = CK nên là hình bình hành.
b) Hình bình hành AHCK có O là trung điểm HK
⇒ O = AC ∩ HK ⇒ A, C, O thẳng hàng.
Đúng 1
Bình luận (0)
1 cach moi la de dang
Trên hình 8,cho ABCD là hình bình hành. Chứng minh rằng AECF là hình bình hành.
Cho hình bình hành ABCD có M, N là trung điểm AB, CD . Gọi P, Q nằm trên cạnh AD, BC
tương ứng sao cho AP=CQ. a. Chứng minh rằng ∆𝑀𝐴𝑃 = ∆𝑁𝐶𝑄. b. Chứng minh rằng ∆𝑀𝐵𝑄 = ∆𝑁𝐷𝑃. c. Chứng minh rằng tứ giác MPNQ là hình bình hành. d. Chứng minh rằng ba đường thẳng MN, PQ, BD đồng quy tại một điể
a: Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(CN=ND=\dfrac{CD}{2}\)
mà AB=CD
nên AM=MB=CN=ND
Xét ΔMAP và ΔNCQ có
MA=CN
\(\widehat{A}=\widehat{C}\)
AP=CQ
Do đó: ΔMAP=ΔNCQ
b: Ta có: BQ+CQ=BC
AP+DP=AD
mà BC=AD
và CQ=AP
nên BQ=DP
Xét ΔMBQ và ΔNDP có
MB=ND
\(\widehat{B}=\widehat{D}\)
BQ=DP
Do đó: ΔMBQ=ΔNDP
Đúng 0
Bình luận (0)



