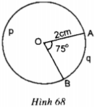
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc AOB = 75o.
Tính độ dài hai cung AqB và ApB
PB
Những câu hỏi liên quan
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc A O B = 75 °
a) Tính sđ góc ApB
b) Tính độ dài hai cung AqB và ApB
c) Tính diện tích hình quạt tròn OAqB
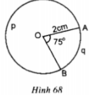
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc AOB = 75o.
Tính sđ A p B ⏜
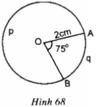
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc AOB = 75o.
Tính diện tích hình quạt tròn OAqB
Cho một điểm M thuộc đường tròn tâm O đường kính R. Vẽ đường tròn tâm O' bán kính r có đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O') ở B.
a) Chứng minh cung MA và cung MB có độ dài bằng nhau.
b) Biết góc AOM = 45 độ và R = 10cm. Tính diện tích giới hạn bởi cung MA, cung MB và đoạn AB.
Cho một điểm M thuộc đường tròn tâm O đường kính R. Vẽ đường tròn tâm O' bán kính r có đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O') ở B.
a) Chứng minh cung MA và cung MB có độ dài bằng nhau.
b) Biết góc AOM = 450 và R = 10cm. Tính diện tích giới hạn bởi cung MA, cung MB và đoạn AB.
H24
Giải mục 1 trang 7 ,8 , 9 SGK Toán 11 tập 1 - Chân trời sáng tạo
16 tháng 7 2023 lúc 16:41
Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được một cung AB có độ dài đúng bằng R (Hình 9). Đo và cho biết \(\widehat {AOB}\) có số đo bằng bao nhiêu độ.
\( \Rightarrow \widehat {AOB} = 60^\circ \)
Đúng 1
Bình luận (0)
cho đường tròn tâm (O) bán kính 3cm trên (O) lấy điểm A,B sao cho góc AOB=60 độ. Tính số đo cung nhỏ AB,diện tích hình quạt tròn OAB,độ dài cung lớn AB
* Số đo cung nhỏ AB=góc AOB( góc ở tâm)\(\Rightarrow\) Số đo cung nhỏ AB=60 độ
* Diện ích hình quạt tròn OAB là
\(S=\frac{\pi\times R2\times n}{360}=\frac{\pi\times9\times60}{360}=\frac{3}{2}\pi\approx\frac{3}{2}\times3,14\approx4,71\)cm2
* Số đo cung lớn AB= 360 độ - 60 độ =300 độ
Độ dài cung lớn AB là:
l=3,14*3*300/180=15,7 cm
Đúng 0
Bình luận (0)
Cho đường tròn (O) đường kính AB. Lấy M thuộc đoạn AB. vẽ dây CD vuông góc với AB tại M. Giả sử AM 2cm và CD
4
3
cm. Tính:a, Độ dài đường tròn (O) và diện tích đường tròn (O)b, Độ dài cung
C
A
D
⏜
và diện tích hình quạt tròn giói hạn bởi hai bán kính OC, OD và cung nhỏ
C...
Đọc tiếp
Cho đường tròn (O) đường kính AB. Lấy M thuộc đoạn AB. vẽ dây CD vuông góc với AB tại M. Giả sử AM = 2cm và CD = 4 3 cm. Tính:
a, Độ dài đường tròn (O) và diện tích đường tròn (O)
b, Độ dài cung C A D ⏜ và diện tích hình quạt tròn giói hạn bởi hai bán kính OC, OD và cung nhỏ C D ⏜
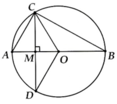
a, AC = 4cm => BC = 4 3 cm
=> R = 4cm => C = 8πcm, S = 16π c m 2
b, ∆AOC đều => A O C ^ = 60 0
=> C O D ^ = 120 0 => l C A D ⏜ = π . 4 . 120 180 = 8 π 3 cm
=> S = 8 π 3 . 4 2 = 16 π 3 c m 2
Đúng 1
Bình luận (0)
Cho đường tròn tâm O bán kính R. Vẽ góc ở tâm AOB = 80 ° , vẽ góc ở tâm BOC = 120 ° kề với góc AOB. So sánh và sắp xếp độ dài AB, BC, CA theo thứ tự tăng dần.
