Cho tập hợp S = (m - 1; m + 1)\(-∞; 1]. Giá trị của m để S chỉ có 1 tập con là:
A. m ≤ 0
B. m < 1
C. m > 1
D. m ≥ 0
PB
Những câu hỏi liên quan
Câu 36. Cho các tập hợp khác rỗng [ m−1; m+3 /2 ] và B=(âm vô cùng ; -3) hợp [3;dương vô cùng). Gọi S là tập hợp các giá nguyên dương của m để A giao B ≠ ∅ . Tìm số tập hợp con của S .
Cho S là tập hợp tất cả caccs giá trị nguyên của tham ssos m sao cho bất phương trình \(\dfrac{(m+1)x^2+\left(4m+2\right)x+4m+4}{mx^2+2\left(2m+1\right)x+m}\le1\) có tập nghiệm là R . Tính số phần tử của tập hợp S
Cho tập hợp M = {1 ; 2 ; 3}
d) Tìm các tập hợp con của tập hợp M
e) Viết tập hợp N gồm các phần tử là các tập hợp con của tập hợp M
f) Khẳng định M là tập hợp con của tập hợp N có đúng không ?
P/s : Nhanh + đúng = tick 😉
Gọi S là tập hợp các giá trị thực của tham số m sao cho phương trình
(
x
+
1
)
3
+
3
-
m
3
3
x
+
m
3
có đúng nghiệm thực. Tích tất cả các phần tử của tập hợp S là A. -1 B. 1 C. 3 D. 5
Đọc tiếp
Gọi S là tập hợp các giá trị thực của tham số m sao cho phương trình ( x + 1 ) 3 + 3 - m = 3 3 x + m 3 có đúng nghiệm thực. Tích tất cả các phần tử của tập hợp S là
A. -1
B. 1
C. 3
D. 5
Cho hàm số
y
2
x
+
1
+
1
2
-
m
với m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m trong khoảng (-50;50) để hàm số nghịch biến trên khoảng (-1;1). Số phần tử của tập hợp S là: A. 47 B. 48 C. 50 D. 49
Đọc tiếp
Cho hàm số y = 2 x + 1 + 1 2 - m với m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m trong khoảng (-50;50) để hàm số nghịch biến trên khoảng (-1;1). Số phần tử của tập hợp S là:
A. 47
B. 48
C. 50
D. 49
Cho hàm số
y
2
x
+
1
+
1
2
x
-
m
với m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m trong khoảng (-50;50) để hàm s...
Đọc tiếp
Cho hàm số y = 2 x + 1 + 1 2 x - m với m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m trong khoảng (-50;50) để hàm số nghịch biến trên khoảng (-1;1). Số phần tử của tập hợp S là:
A. 47
B. 48
C. 50
D. 49
MN
29 tháng 5 2020 lúc 22:38
Cho S là tập hợp tất cả các giá trị nguyên của tham số m sao cho bất phương trình: \(\frac{\left(m+1\right)x^2+\left(4m+2\right)x+4m+4}{mx^2+2\left(m+1\right)x+m}\le1\) có tập nghiệm là R. Tìm số phần tử của tập hợp S
\(\frac{\left(m+1\right)x^2+\left(4m+2\right)x+4m+4}{mx^2+2\left(m+1\right)x+m}-1\le0\)
\(\Leftrightarrow\frac{x^2+2mx+3m+4}{mx^2+2\left(m+1\right)x+m}\le0\)
Để tập nghiệm của BPT đã cho là R
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+2mx+3m+4\ge0\\mx^2+2\left(m+1\right)x+m< 0\end{matrix}\right.\) \(\forall x\in R\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'_1=m^2-3m-4\le0\\m< 0\\\Delta'_2=\left(m+1\right)^2-m^2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le m\le4\\m< 0\\2m+1< 0\end{matrix}\right.\) \(\Rightarrow-1\le m< -\frac{1}{2}\)
Đúng 0
Bình luận (2)
Cho hàm số
y
2
x
3
+
3
(
m
−
1
)
x
2
+
6
(
m
−
2
)
x
−
1
. Gọi S là tập hợp tất cả các giá trị thực của m để hàm số có hai điểm cực trị đều thuộc (-2;1). Khi đó tập S là A. S (1;4) B.
S
ℝ
3
C. ...
Đọc tiếp
Cho hàm số y = 2 x 3 + 3 ( m − 1 ) x 2 + 6 ( m − 2 ) x − 1 . Gọi S là tập hợp tất cả các giá trị thực của m để hàm số có hai điểm cực trị đều thuộc (-2;1). Khi đó tập S là
A. S = (1;4)
B. S = ℝ \ 3
C. S = − ∞ ; 1 ∪ 4 ; + ∞
D. S = ( 1 ; 4 ) \ 3
Cho hàm số
f
(
x
)
ax
3
+
bx
2
+
cx
+
d
có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị của m(m∈R) sao cho (x-1)
[
m
3
f
(
2
x
-
1
)
-
mf
(
x
)
+
f
(
x
)...
Đọc tiếp
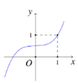
Cho hàm số f ( x ) = ax 3 + bx 2 + cx + d có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị của m(m∈R) sao cho (x-1) [ m 3 f ( 2 x - 1 ) - mf ( x ) + f ( x ) - 1 ] ≥0 ∀x∈R. Số phần tử của tập S là
A. 2
B. 0
C. 3
D. 1
