Trong các mệnh đề sau
a. Phương trình 2 - x = x có nghiệm x = – 2.
b. 7 - 4 3 = 3 - 2 .
c. 2 x - 1 x - 2 = x + 1 x - 2 vô nghiệm.
d. ∀ x ∈ ℝ , 5 x 2 - 4 5 x + 3 ⩽ - 1 .
Số mệnh đề đúng là:
A. 4.
B. 2
C. 3
D. 1
Cho hệ bất phương trình x - 7 ≤ 0 mx ≥ m + 1
Xét các mệnh đề sau :
(1) : Với m< 0 , hệ luôn có nghiệm.
(2) : Với 0 ≤ m < 1/6 hệ vô nghiệm.
(3) : Với m = 1/6 hệ có nghiệm duy nhất.
Mệnh đề nào đúng?
A. Chỉ (1)
B. (2) và (3)
C. Chỉ (3)
D. (1) ; (2) và (3)
Cho hệ bất phương trình x - 7 ≤ 0 m x ≥ m + 1 . Xét các mệnh đề sau
(1) Với m< 0 , hệ luôn có nghiệm.
(2) Với 0 ≤ m < 1/6 hệ vô nghiệm.
(3) Với m= 1/6 , hệ có nghiệm duy nhất.
Mệnh đề nào đúng?
A. Chỉ (1)
B. (2) và (3)
C. Chỉ (3)
D . Cả ba đúng
Cho các mệnh sau
(I) 5 là nghiệm của phương trình 2x – 3 = x + 2 x - 4
(II) Tập nghiệm của phương trình 7 – x = 2x – 8 là x = 5
(III) Tập nghiệm của phương trình 10 – 2x = 0 là S = {5}.
Số mệnh đề đúng là:
A. 1
B. 0
C. 2
D. 3
+) Thay x = 5 vào phương trình 2 x − 3 = x + 2 x − 4 ta được
2.5 − 3 = 5 + 2 5 − 4 ⇔ 7 = 7 1 = 7
Vậy 5 là nghiệm của phương trình 2 x − 3 = x + 2 x − 4 khẳng định (I) đúng.
+) Tập nghiệm của phương trình 7 – x = 2x – 8 là x = 5 là khẳng định sai vì kết luận x = 5 không phải là tập nghiệm.
+) Ta có: 10 - 2x = 0 ⇔ 2x = 10 ⇔ x = 5
Vậy tập nghiệm của phương trình là S = {5}.
Do đó khẳng định (III) là đúng.
Vậy có hai mệnh đề đúng.
Đáp án cần chọn là: C
Cho hàm số y = f x xác định, có đạo hàm trên đoạn a ; b (với a < b ). Xét các mệnh đề sau:
i) Nếu f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên khoảng a ; b .
ii) Nếu phương trình f ' ( x ) = 0 có nghiệm x 0 thì f ' ( x ) đổi dấu từ dương sang âm khi qua x 0 .
iii) Nếu f ' x ≤ 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
Số mệnh đề đúng trong các mệnh đề trên là:
A. 2
B. 3
C. 0
D. 1
Chọn D
i) Đúng.
ii) Sai, ví dụ: Xét hàm số
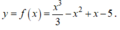
Ta có f ' x = x 2 - 2 x + 1 .
Cho f ' ( x ) ⇔ x = 1 .
Khi đó phương trình f ' ( x ) = 0 có nghiệm x 0 = 1 nhưng đây là nghiệm kép nên không đổi dấu khi qua x 0 .
iii) Sai, vì: Thiếu điều kiện f ' ( x ) = 0 chỉ tại một số hữu hạn điểm.
Vậy có 1 mệnh đề đúng.
Cho các mệnh đề:
1. Nếu hàm số y=f(x) liên tục trên a ; b và f a . f b < 0 thì tồn tại x 0 ∈ a ; b sao cho f x 0 = 0.
2. Nếu hàm số y = f x liên tục trên a ; b và f a . f b < 0 thì phương trình f x = 0 có nghiệm.
3. Nếu hàm số y=f(x) liên tục, đơn điệu trên a ; b và f a . f b < 0 thì phương trình f x = 0 có nghiệm duy nhất trên ( a ; b ) .
Trong ba mệnh đề trên
A. Có đúng hai mệnh đề sai
B. Cả ba mệnh đề đều đúng
C. Cả ba mệnh đề đều sai
D. Có đúng một mệnh đề sai
Đáp án D
Định lí: “Nếu hàm số y = f x liên tục trên a ; b và f a . f b < 0 thì tồn tại ít nhất một điểm c ∈ a ; b sao cho f c = 0 ”.
Mệnh đề 1: SAI ở giả thiết (a;b).
Mệnh đề 2: Nếu hàm số y=f(x) liên tục trên a ; b
và f a . f b < 0 thì tồn tại ít nhất một điểm c ∈ a ; b sao cho c hay f x = 0 là nghiệm của phương trình f(x)=0 nên mệnh đề 2 ĐÚNG.
Mệnh đề 3: Nếu hàm số y=f(x) liên tục, đơn điệu trên a ; b và f a . f b < 0 thì đồ thị hàm số y=f(x) cắt trục Ox tại duy nhất một điểm thuộc khoảng (a;b) nên f(x)=0 có nghiệm duy nhất trên (a;b). Do đó mệnh đề 3 ĐÚNG
Lập mệnh đề phủ định của mỗi mệnh đề sau và nhận xét tính đúng sai của mệnh đề phủ định đó.
a) A: “\(\frac{5}{{1,2}}\) là một phân số”.
b) B: “Phương trình \({x^2} + 3x + 2 = 0\) có nghiệm”.
c) C: “\({2^2} + {2^3} = {2^{2 + 3}}\)”.
d) D: “Số 2 025 chia hết cho 15”.
a) \(\overline A \): “\(\frac{5}{{1,2}}\) không là một phân số”.
Đúng vì \(\frac{5}{{1,2}}\) không là phân số (do 1,2 không là số nguyên)
b) \(\overline B \): “Phương trình \({x^2} + 3x + 2 = 0\) vô nghiệm”.
Sai vì phương trình \({x^2} + 3x + 2 = 0\) có hai nghiệm là \(x = - 1\) và \(x = - 2\).
c) \(\overline C \): “\({2^2} + {2^3} \ne {2^{2 + 3}}\)”.
Đúng vì \({2^2} + {2^3} = 12 \ne 32 = {2^{2 + 3}}\).
d) \(\overline D \): “Số 2 025 không chia hết cho 15”.
Sai vì 2025 = 15. 135, chia hết cho 15.
Gọi S là tập nghiệm của phương trình \({x^2} - 24x + 143 = 0\).
Các mệnh đề sau đúng hay sai?
a) \(13 \in S\)
b) \(11 \notin S\)
c) \(n\;(S) = 2\)
a) Vì \({13^2} - 24.13 + 143 = 0\) nên \(x = 13\) là nghiệm của phương trình \( \Rightarrow 13 \in S\)
Vậy mệnh đề “\(13 \in S\)” đúng.
b) Vì \({11^2} - 24.11 + 143 = 0\) nên \(x = 11\) là nghiệm của phương trình \( \Rightarrow 11 \in S\)
Vậy mệnh đề “\(11 \notin S\)” sai.
c) Ta có:
\(\begin{array}{l}{x^2} - 24x + 143 = 0\\ \Leftrightarrow {x^2} - 11x - 13x + 11.13 = 0\\ \Leftrightarrow x.\left( {x - 11} \right) - 13.\left( {x - 11} \right) = 0\\ \Leftrightarrow \left( {x - 11} \right).\left( {x - 13} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 11\\x = 13\end{array} \right.\end{array}\)
Tập nghiệm của phương trình là \(S=\{11;13\}\)
Phương trình có 2 nghiệm hay \(n\;(S) = 2\)
=> Mệnh đề “\(n\;(S) = 2\)” đúng.
Cho hàm số f x = x 5 + x − 1 . Trong các mệnh đề sau, mệnh đề nào là SAI khi nói về nghiệm thực của phương trình f x = 0 ?
A. Phương trình có nghiệm trong khoảng 0 ; 1
B. Phương trình có duy nhất một nghiệm
C. Phương trình có đúng 5 nghiệm
D. Phương trình có nghiệm trong khoảng − 1 ; 1
Cho hàm số f x = 3 2 x - 2 . 3 x có đồ thị như hình vẽ sau
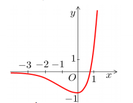
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Đường thẳng y = 0 cắt đồ thị hàm số (C) tại điểm có hoành độ là x = log 3 2
(2) Bất phương trình f x ≥ - 1 có nghiệm duy nhất.
(3) Bất phương trình f x ≥ 0 có tập nghiệm là - ∞ ; log 3 2
(4) Đường thẳng y = 0 cắt đồ thị hàm số (C) tại 2 điểm phân biệt.
A. 2
B. 4
C. 1
D. 3
Đáp án C
Dựa vào đáp án, ta thấy rằng
(1) Đường thẳng f x = 0 ⇔ 3 2 x - 2 . 3 x = 0 ⇔ 3 x = 2 ⇔ x = log 3 2 ⇒ 1 đúng.
(2) Bất phương trình f x ≥ - 1 ⇔ 3 2 x - 2 . 3 x + 1 ≥ 0 ⇔ 3 x - 1 2 ≥ 0 , ∀ x ∈ ℝ . Nên f x ≥ - 1 có vô số nghiệm ⇒ 2 sai.
(3) Bất phương trình f x ≥ 0 ⇔ 3 x 2 - 2 . 3 x ≥ 0 ⇔ 3 x ≥ 2 ⇔ x ≥ log 3 2 ⇒ 3 sai.
(4) Đường thẳng f(x) = 0 chỉ có 1 nghiệm duy nhất ⇒ 4 sai