Cho ΔDEF ∼ ΔABC biết DE = 5cm, AB = 6cm, AC = 12cm. Độ dài DF là:
A. 8cm
B. 9cm
C. 10cm
D. 15cm
PB
Những câu hỏi liên quan
cho ΔDEF∼ΔABC. Biết AB=12cm, BC=15cm và DE=4cm. độ dài đoạn thẳng EF là
Ta có tỉ số : \(\dfrac{DE}{AB}=\dfrac{EF}{BC}\Rightarrow\dfrac{4}{12}=\dfrac{EF}{15}\Rightarrow EF=\dfrac{15\times4}{12}=5\)
Vậy \(EF=5cm\)
Đúng 6
Bình luận (0)
Cho tam giác ABC vuông tại A, có AB = 6cm, AC = 8cm , BC = 10cm và tam giác DEF vuông tại D có DE = 9cm, DF = 12cm, EF = 15cm.
a) Hai tam giác ABC và DEF có đồng dạng không? Vì sao?
b) Tính tỉ số chu vi của hai tam giác ấy?
a: Xét ΔABC vuông tại A và ΔDEF vuông tại D có
AB/DE=AC/DF
Do đó: ΔABC\(\sim\)ΔDEF
b: \(\dfrac{C_{ABC}}{C_{DEF}}=\dfrac{AB}{DE}=\dfrac{2}{3}\)
Đúng 0
Bình luận (0)
1) cho ΔABC ∼ ΔDEF theo tỉ số đồng dạng kdfrac{3}{2} . Diện tích ΔABC là 27 cm^2, thi diện tích ΔDEF là:A. 12cm^2 B.24cm^2 C. 36cm^2 D. 18cm^22) ΔABC ∼ΔDEF có AB3cm, AC5cm, BC7cm, DE6cm. Ta có :A. DF10cm B. DF20cm C. EF14cm D.EF10cm
Đọc tiếp
1) cho ΔABC ∼ ΔDEF theo tỉ số đồng dạng k=\(\dfrac{3}{2}\) . Diện tích ΔABC là 27 cm\(^2\), thi diện tích ΔDEF là:
A. 12cm\(^2\) B.24cm\(^2\) C. 36cm\(^2\) D. 18cm\(^2\)
2) ΔABC ∼ΔDEF có AB=3cm, AC=5cm, BC=7cm, DE=6cm. Ta có :
A. DF=10cm B. DF=20cm C. EF=14cm D.EF=10cm
Xem thêm câu trả lời
Cho Δ A B C = Δ D E F . Biết rằng AB=6cm; AC=8cm, EF=10cm. Tính chu vi tam giác DEF là
A. 24cm
B. 20cm
C. 18 cm
D. 30 cm
Hai tam giác ABC và DEF có góc A = góc D, góc B = góc E, AB = 8cm, BC = 10cm, DE =6cm. Tính độ dài các cạnh AC, DF và EF, biết rằng cạnh AC dài hơn cạnh DF là 3cm.
Hai tam giác ABC và DEF có góc A = góc D, góc B = góc E, AB = 8cm, BC = 10cm, DE =6cm. Tính độ dài các cạnh AC, DF và EF, biết rằng cạnh AC dài hơn cạnh DF là 3cm.
Hai tam giác mà các cạnh có độ dài sau đây thì đồng dạng với nhau. Trường hợp nào đúng ? Trường hợp nào sai ? hãy đánh dấu gạch chéo vào ô trả lời thích hợp ở bảng sau:
Trường hợp
Đúng
Sai
a. 1,5cm, 2cm, 3cm và 4,5cm, 6cm, 9cm.
b. 2,5cm, 4cm, 5cm và 5cm, 12cm, 8cm.
c. 3,5cm, 6cm, 7cm và 15cm, 12cm, 7cm.
d. 2cm, 5cm, 6,5cm và 13cm, 10cm, 4cm.
Đọc tiếp
Hai tam giác mà các cạnh có độ dài sau đây thì đồng dạng với nhau. Trường hợp nào đúng ? Trường hợp nào sai ? hãy đánh dấu gạch chéo vào ô trả lời thích hợp ở bảng sau:
| Trường hợp | Đúng | Sai |
| a. 1,5cm, 2cm, 3cm và 4,5cm, 6cm, 9cm. | ||
| b. 2,5cm, 4cm, 5cm và 5cm, 12cm, 8cm. | ||
| c. 3,5cm, 6cm, 7cm và 15cm, 12cm, 7cm. | ||
| d. 2cm, 5cm, 6,5cm và 13cm, 10cm, 4cm. |
Cho ΔABC = ΔDEF. Tính chu vi mỗi tam giác nói trên biết rằng AB = 4cm, BC = 6cm, DF = 5cm (chu vi mỗi tam giác là tổng độ dài ba cạnh của tam giác đó).
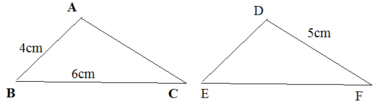
Vì ΔABC = ΔDEF nên suy ra:
AB = DE = 4cm
BC = EF = 6cm
DF = AC = 5cm
Chu vi tam giác ABC bằng:
AB + BC + CA = 4 + 6 + 5 = 15 (cm)
Chu vi tam giác DEF bằng:
DE + EF + DF = 4 + 6 + 5 = 15 (cm)
Đúng 0
Bình luận (0)
Các tam giác với số đo của các cạnh như sau có phải là tam giác vuông không? Vì sao? Nếu có thì vuông tại đỉnh nào?
a/AB = 15cm, CB = 12cm, AC = 9cm
b/DE = 6cm, EF = 8cm, DF = 10cm
a: Vì \(CB^2+CA^2=AB^2\)
nên ΔCBA vuông tại C
b: Vì \(DF^2=ED^2+EF^2\)
nên ΔDEF vuông tại E
Đúng 0
Bình luận (0)