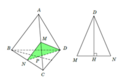
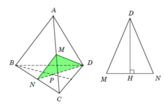
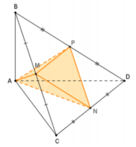
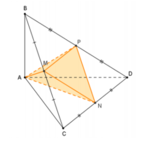
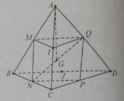
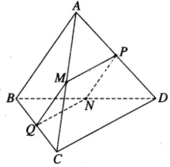
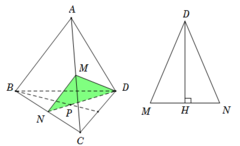
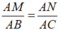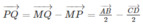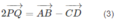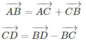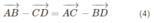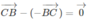Cho tứ diện ABCD có M, N lần lượt là trung điểm của các cạnh AC, BC. Điểm P thỏa mãn P B → + 2 P D → = 0 → và điểm Q là giao điểm của hai đường thẳng CD và NP. Hỏi đường thẳng nào sau đây là giao tuyến của hai mp (MNP) và (ACD)?
A. CQ
B. MQ
C. MP
D. NQ