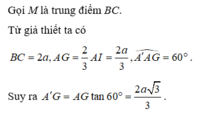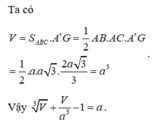Cho tam giác ABC vuông tại A .Gọi V 1 , V 2 , V 3 theo thứ tự là thể tích của những hình sinh ra khi quay tam giác ABC một vòng xung quanh các cạnh BC , AB và AC.Chứng minh rằng : 1 V 1 2 = 1 V 2 2 + 1 V 2 2
PB
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Gọi \(V_1,V_2,V_3\) theo thứ tự là thể tích của những hình sinh ra khi quay tam giác ABC một vòng xung quanh các cạnh BC, AB và AC. Chứng minh rằng :
\(\dfrac{1}{V^2_1}=\dfrac{1}{V^2_2}+\dfrac{1}{V^2_3}\)
cho tam giác abc vuông tại a .gọi g là trung điểm bc từ g kẻ ge vuông góc với ab ,gf vuông góc ac từ e kẻ đường thẳng song song với bf đường thẳng này cắt bf tại i cho tam giác abc vuông tại a .gọi g là trung điểm bc từ g kẻ ge vuông góc với ab ,gf vuông góc ac từ e kẻ đường thẳng song song với bf đường thẳng này cắt bf tại i A chứng minh tứ giác AEFG là hình chữ nhật B chứng minh tứ giác BEIF là hình bình hành C chứng minh tứ giác AGCI là hình thoi
Đọc tiếp
cho tam giác abc vuông tại a .gọi g là trung điểm bc từ g kẻ ge vuông góc với ab ,gf vuông góc ac từ e kẻ đường thẳng song song với bf đường thẳng này cắt bf tại i cho tam giác abc vuông tại a .gọi g là trung điểm bc từ g kẻ ge vuông góc với ab ,gf vuông góc ac từ e kẻ đường thẳng song song với bf đường thẳng này cắt bf tại i A chứng minh tứ giác AEFG là hình chữ nhật B chứng minh tứ giác BEIF là hình bình hành C chứng minh tứ giác AGCI là hình thoi
Sửa đề: Từ E kẻ đường thẳng song song với BF, cắt GF tại I
a: Xét tứ giác AEGF có
\(\widehat{AEG}=\widehat{AFG}=\widehat{FAE}=90^0\)
Do đó: AEGF là hình chữ nhật
b: AEGF là hình chữ nhật
=>GF//AE và GF=AE
Ta có: GF//AE
I\(\in\)FG
Do đó: FI//AE
Ta có: FI//AE
E\(\in\)AB
Do đó: FI//EB
Xét tứ giác FIEB có
FI//EB
FB//EI
Do đó: FIEB là hình bình hành
c: Xét ΔABC có
G là trung điểm của BC
GE//AC
Do đó: E là trung điểm của AB
=>EA=EB(1)
Xét ΔABC có
G là trung điểm của BC
GF//AB
Do đó: F là trung điểm của AC
AEGF là hình chữ nhật
=>AE=GF(2)
FIEB là hình bình hành
=>FI=EB(3)
Từ (1),(2),(3) suy ra FI=FG
=>F là trung điểm của GI
Xét tứ giác AGCI có
F là trung điểm chung của AC và GI
nên AGCI là hình bình hành
Hình bình hành AGCI có AC\(\perp\)GI
nên AGCI là hình thoi
Đúng 2
Bình luận (0)
Cho lăng trụ tam giác ABC.ABC có đáy ABC là tam giác vuông tại A với AB a, AC
a
3
. Hình chiếu vuông góc của A lên mặt phẳng (ABC) trùng với trọng tâm G của tam giác ABC và góc giữa AA’ tạo với mặt phẳng (ABC) bằng
60
∘
. Gọi V là thể tích khối lăng trụ ABC.ABC. Tính
V
3
+
V
a
3
-
1...
Đọc tiếp
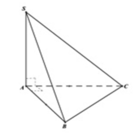
Cho lăng trụ tam giác ABC.A'B'C' có đáy ABC là tam giác vuông tại A với AB = a, AC = a 3 . Hình chiếu vuông góc của A' lên mặt phẳng (ABC) trùng với trọng tâm G của tam giác ABC và góc giữa AA’ tạo với mặt phẳng (ABC) bằng 60 ∘ . Gọi V là thể tích khối lăng trụ ABC.A'B'C'. Tính V 3 + V a 3 - 1 .
A. 1.
B. a.
C. a 2 .
D. a 3 .
Cho lăng trụ tam giác ABC.ABC có đáy ABC là tam giác vuông tại A với AB a; AC
a
3
. Hình chiếu vuông góc của A’ lên mặt phẳng (ABC) trùng với trọng tâm G của tam giác ABC và góc giữa AA’ tạo với mặt phẳng ( ABC ) bằng
60
o
. Gọi V là thể tích khối lăng trụ ABC.ABC. Tính
V
3
+
V
a
3...
Đọc tiếp
Cho lăng trụ tam giác ABC.A'B'C' có đáy ABC là tam giác vuông tại A với AB = a; AC = a 3 . Hình chiếu vuông góc của A’ lên mặt phẳng (ABC) trùng với trọng tâm G của tam giác ABC và góc giữa AA’ tạo với mặt phẳng ( ABC ) bằng 60 o . Gọi V là thể tích khối lăng trụ ABC.A'B'C'. Tính V 3 + V a 3 - 1
A. 1
B. a
C. a 2
D. a 3
Gọi M là trung điểm BC: BC = 2a; AG = 2 3 AI = 2 a 3 ; A ' A G ^ = 60 o .
Suy ra: A ' G = A G tan 60 o = 2 a 3 3
Ta có: V = S A B C . A ' G = 1 2 AB.AC.A'G
= 1 2 a. a 3 . 2 a 3 3 = a 3
Vậy V 3 + V a 3 - 1 = a
Đáp án B
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy (ABC). Biết SAa tam giác ABC là tam giác vuông cân tại A, AB2a. Tính theo a thể tích V của khối chóp S.ABC
Đọc tiếp
Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy (ABC). Biết SA=a tam giác ABC là tam giác vuông cân tại A, AB=2a. Tính theo a thể tích V của khối chóp S.ABC
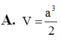
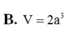
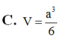
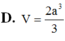
Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy (ABC). Biết SAa tam giác ABC là tam giác vuông cân tại A, AB2a. Tính theo a thể tích V của khối chóp S.ABC. A.
V
a
3
2
B.
V
2
a
3
C.
V
a
3...
Đọc tiếp
Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy (ABC). Biết SA=a tam giác ABC là tam giác vuông cân tại A, AB=2a. Tính theo a thể tích V của khối chóp S.ABC.
A. V = a 3 2
B. V = 2 a 3
C. V = a 3 6
D. 2 a 3 3
Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy
A
B
C
. Biết
S
A
a
tam giác ABC là tam giác vuông cân tại A,
A
B
2
a
. Tính theo a thể tích V của khối chóp S.ABC.
Đọc tiếp
Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy A B C . Biết S A = a tam giác ABC là tam giác vuông cân tại A, A B = 2 a . Tính theo a thể tích V của khối chóp S.ABC.
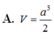
![]()
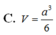
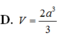
Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy (ABC). Biết SA a, tam giác ABC là tam giác vuông cân tại A, AB 2a. Tính theo a thể tích V của khối chóp S.ABC A.
V
a
3
2
B.
V
2
a
3
C.
V
a
3
6
D.
V...
Đọc tiếp
Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy (ABC). Biết SA= a, tam giác ABC là tam giác vuông cân tại A, AB = 2a. Tính theo a thể tích V của khối chóp S.ABC
A. V = a 3 2
B. V = 2 a 3
C. V = a 3 6
D. V = 2 a 3 3
Đáp án D
Thể tích hình chóp là: V = 1 3 S A . S A B C = 1 3 . a . 1 2 2 a 2 = 2 a 3 3
Đúng 0
Bình luận (0)
Mình cần gấp ạ....
1)Cho tam giác ABC cân tại A có AB=6 cm,BC=4 cm.Tính các góc trong tam giác ABC.
2)Cho tam giác ABC vuông tại A có góc B=50 độ,BC=5 cm.Ở phía ngoài tam giác ABC,vẽ tam giác vuông ADC có góc CAD=35 độ.Tính chu vi tam giác ABC và chu vi tam giác ADC
câu 1: tìm x biết(2x - 1)2 - (x+3)2 0câu 2: Cho tam giác ABC vuông tại A ( ABAC), đường cao AH ( H ϵ BC). Kẻ HE vuông góc với AB ( E ϵ BC ) và HF vuông góc với AC ( F ϵ AC).a) chứng minh tứ giác AEHF là hình chữ nhậtb) gọi O là giao điểm của AH và EF, M là trung điểm của AC. Qua F kẻ đường thẳng vuông góc với EF cắt BC tại N. Chứng minh ON//AC và chứng minh tứ giác AONM là hình bình hành.c) Gọi EF cắt NM tại I. Chứng minh tam giác ONI cân
Đọc tiếp
câu 1: tìm x biết
(2x - 1)2 - (x+3)2 = 0
câu 2: Cho tam giác ABC vuông tại A ( AB<AC), đường cao AH ( H ϵ BC). Kẻ HE vuông góc với AB ( E ϵ BC ) và HF vuông góc với AC ( F ϵ AC).
a) chứng minh tứ giác AEHF là hình chữ nhật
b) gọi O là giao điểm của AH và EF, M là trung điểm của AC. Qua F kẻ đường thẳng vuông góc với EF cắt BC tại N. Chứng minh ON//AC và chứng minh tứ giác AONM là hình bình hành.
c) Gọi EF cắt NM tại I. Chứng minh tam giác ONI cân