
 nãy em chọn lộn môn hoá em xin lỗi ạ :> mọi ngừoi giúp em với em cần gấp ạ
nãy em chọn lộn môn hoá em xin lỗi ạ :> mọi ngừoi giúp em với em cần gấp ạ
H24
Những câu hỏi liên quan
Mọi ngừoi giúp em với em đang cần gấp ạ
a/ Ta có
- \(Cl=35,5đvC\)
- Đơn chất \(Cl=71đvC\)
- Số nguyên tử Cl trong 1 phân tử Cl \(=\dfrac{71}{35,5}=2\)
Vậy: Số nguyên tử Cl trong 1 phân tử Cl là 2
Đúng 1
Bình luận (0)
Giúp em với ạ ! em đang cần gấp , chọn lỗi sai xong sửa luôn với ạ 
1. is -> was
2. depressing -> depressed
3. has gone -> had gone
4. was opening -> opened
5. attending -> to attend
6. tomorrow -> the next day
7. two - days -> two - day
8. do i want -> i wanted
9. câu này hình như thiếu đề ạ
10. will we -> shall we
Đúng 0
Bình luận (2)

Xin lỗi mọi người nãy em copy nên không có ảnh ạ
Bài 10:
a: Để A có nghĩa thì \(\dfrac{2x+5}{x-3}\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+5\le0\\x-3>0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\le-\dfrac{5}{2}\\x>3\end{matrix}\right.\)
Để B có nghĩa thì \(\left\{{}\begin{matrix}2x+5\ge0\\x-3>0\end{matrix}\right.\Leftrightarrow x>3\)
b: Để A=B thì \(\sqrt{\dfrac{2x+5}{x-3}}=\dfrac{\sqrt{2x+5}}{\sqrt{x-3}}\)
\(\Leftrightarrow\dfrac{2x+5}{x-3}=\dfrac{2x+5}{x-3}\)(luôn đúng với mọi x thỏa mãn ĐKXĐ
Đúng 1
Bình luận (0)
Cần gấp ạ, xin mọi người giúp em vs ạ. Em cảm ơn mọi người. Nếu đc em xin cả cách giải ạ


Hướng dẫn: A đạt GTLN khi \(\dfrac{1}{A}\) đạt GTNN
Ta có: \(x^2+2\ge0\forall x\)
\(\Rightarrow A=\dfrac{1}{x^2+2}\le\dfrac{1}{2}\forall x\)
Vậy GTLN của A là 1/2
=> A
Đúng 2
Bình luận (1)
Câu 2: B đạt GTLN khi và chỉ khi x2 đạt giá trị nhỏ nhất
⇔ x2=0 ⇒B = 10 - 0= 0
Chọn đáp án B nhe
Câu 3: Có A= 4x - 2x2= (-2x2 + 4x - 1) + 1=\(-2\left(x^2-2x+1\right)+1\)
⇔ A= \(-2\left(x-1\right)^2+1\le1\)
Chọn đáp án B nha
Đúng 2
Bình luận (0)
Mọi người giúp em với ạ, nếu đc thù em xin cả cách giải, em đang cần gấp lắm ạ, cảm ơn mọi người nhiều


Câu 1: A
Câu 2: B
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Câu 7: A
Câu 9: B
Đúng 1
Bình luận (0)
Nhờ mọi người giúp vs, em đg cần gấp ạ, cho em xin cả cách giải với ạ. Em cảm ơn mọ người


Có ai ko giúp em với . Em đang cần rất gấp trước 3h00 ạ . Em mong mọi người giúp em . Em xin cảm ơn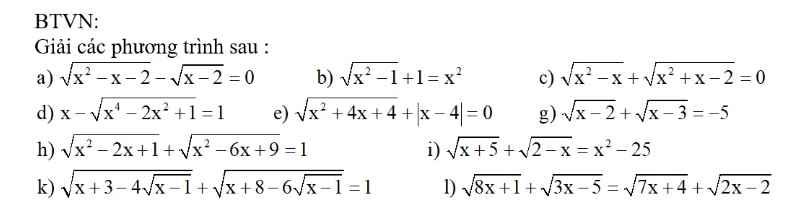
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\le-1\\x\ge2\end{matrix}\right.\)
\(\sqrt{x^2-x-2}-\sqrt{x-2}=0\\ \Leftrightarrow\sqrt{x^2-x-2}=\sqrt{x-2}\\ \Leftrightarrow x^2-x-2=x-2\\ \Leftrightarrow x^2-2x=0\\ \Leftrightarrow x\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=2\left(tm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
\(a,ĐK:x\ge2\\ PT\Leftrightarrow x^2-x-2=x-2\\ \Leftrightarrow x^2-2x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=0\left(ktm\right)\end{matrix}\right.\Leftrightarrow x=2\\ b,ĐK:\left[{}\begin{matrix}x\le-1\\x\ge1\end{matrix}\right.\\ PT\Leftrightarrow\sqrt{x^2-1}=x^2-1\\ \Leftrightarrow x^2-1=\left(x^2-1\right)^2\\ \Leftrightarrow\left(x^2-1\right)\left(x^2-1-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-1\left(tm\right)\\x=\sqrt{2}\left(tm\right)\\x=-\sqrt{2}\left(tm\right)\end{matrix}\right.\)
\(c,ĐK:\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\\ PT\Leftrightarrow\sqrt{x^2-x}=-\sqrt{x^2+x-2}\\ \Leftrightarrow x^2-x=x^2+x-2\\ \Leftrightarrow2x=2\\ \Leftrightarrow x=1\left(tm\right)\)
Đúng 1
Bình luận (0)
\(d,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{\left(x^2-1\right)^2}=x-1\\ \Leftrightarrow\left|x^2-1\right|=x-1\\ \Leftrightarrow\left[{}\begin{matrix}x^2-1=x-1\left(x\le-1;x\ge1\right)\\x^2-1=1-x\left(-1< x< 1\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=0\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\\\left[{}\begin{matrix}x=1\left(ktm\right)\\x=-2\left(ktm\right)\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
\(e,PT\Leftrightarrow\left|x+2\right|+\left|x-4\right|=0\Leftrightarrow\left\{{}\begin{matrix}x+2=0\\x-4=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=-2\\x=4\end{matrix}\right.\Leftrightarrow x\in\varnothing\)
\(g,\Leftrightarrow x\in\varnothing\left(\sqrt{x-2}+\sqrt{x-3}\ge0>-5\right)\\ f,\Leftrightarrow\left|x-1\right|+\left|x-3\right|=1\\ \Leftrightarrow\left[{}\begin{matrix}1-x+3-x=1\left(x< 1\right)\\x-1+3-x=1\left(1\le x< 3\right)\\x-1+x-3=1\left(x\ge3\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\left(ktm\right)\\0x=-1\left(ktm\right)\\x=\dfrac{5}{2}\left(ktm\right)\end{matrix}\right.\\ \Leftrightarrow x\in\varnothing\)
Đúng 1
Bình luận (0)
Làm giúp e với ạ
Em cần gấp xin mọi người ạ
Em đang cần gấp nên mong mọi người giúp với ạ em xin cảm ơn









