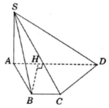
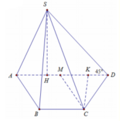
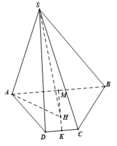
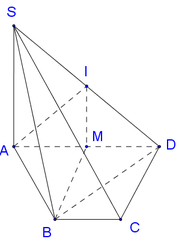
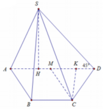
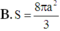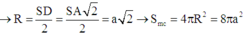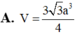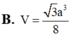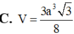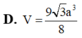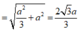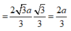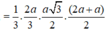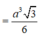Cho hình chóp S.ABCD có ABCD là hình thang cân (AD//BC) và BC = 2AD = 2a, A B C ^ = 60 ° . Gọi M, N, E lần lượt là trung điểm của AB, CD, SA. SA ⊥ (ABCD) và SA = a 2 . Khoảng cách giữa hai mặt phẳng (MNE) và (SBC) là:
A. 2 a 66 11
B. a 66 11
C. a 66 22
D. 3 a 66 22