Đáp án C

Theo tỉ số thể tích ta có:

Tự vẽ hình nhé!

Ta có:

\(V_{OBCNM}=\dfrac{1}{3}d\left(O;\left(BCNM\right)\right).S_{BCNM}=\dfrac{1}{3}.\dfrac{1}{2}d\left(A;\left(SBC\right)\right).\dfrac{3}{4}S_{SBC}=\dfrac{1}{8}V_{SABC}=\dfrac{1}{16}V_{SABCD}\)

\(\Rightarrow\dfrac{V_{OBCNM}}{V_{SABCD}}=\dfrac{1}{16}\)

Do (MAB) chứa AB // CD, nên giao tuyến của (MAB) với (SCD) là đường thẳng đi qua M và song song với AB. Đường thẳng này cắt SD tại điểm N.

Vậy thiết diện của (MAB) với hình chóp là tứ giác ABMN, với N là giao điểm của SD với đường thẳng đi qua M và song song với AB.

Đáp án B

Nối AN kéo dài cắt CD tại E, nối EM kéo dài cắt SD tại I

Do N là trung điểm OB \(\Rightarrow\dfrac{BN}{ND}=\dfrac{1}{3}\)

Áp dụng định lý talet: \(\dfrac{BF}{AD}=\dfrac{BN}{ND}=\dfrac{1}{3}\) \(\Rightarrow\dfrac{CF}{AD}=\dfrac{2}{3}\)

Cũng theo Talet:

\(\dfrac{FC}{FD}=\dfrac{CF}{AD}=\dfrac{2}{3}\) \(\Rightarrow\dfrac{DF}{FC}=\dfrac{3}{2}\)

Áp dụng định lý Menelaus cho tam giác SCD:

\(\dfrac{IS}{ID}.\dfrac{DF}{FC}.\dfrac{CM}{MS}=1\Rightarrow\dfrac{IS}{ID}.\dfrac{3}{2}.1=1\Rightarrow\dfrac{IS}{ID}=\dfrac{2}{3}\)

\(\Rightarrow\dfrac{SI}{SD}=\dfrac{2}{5}\)

Chọn B

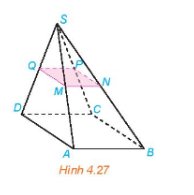
Xét tam giác SAB ta có: MN là đường trung bình suy ra MN // AB.

Tương tự ta có: NP // BC, PQ // CD, MQ // AD.

Mà ABCD là hình bình hành nên AB // CD, AD// CD, suy ra MN // PQ, MQ // NP.

Như vậy, MNPQ là hình bình hành.

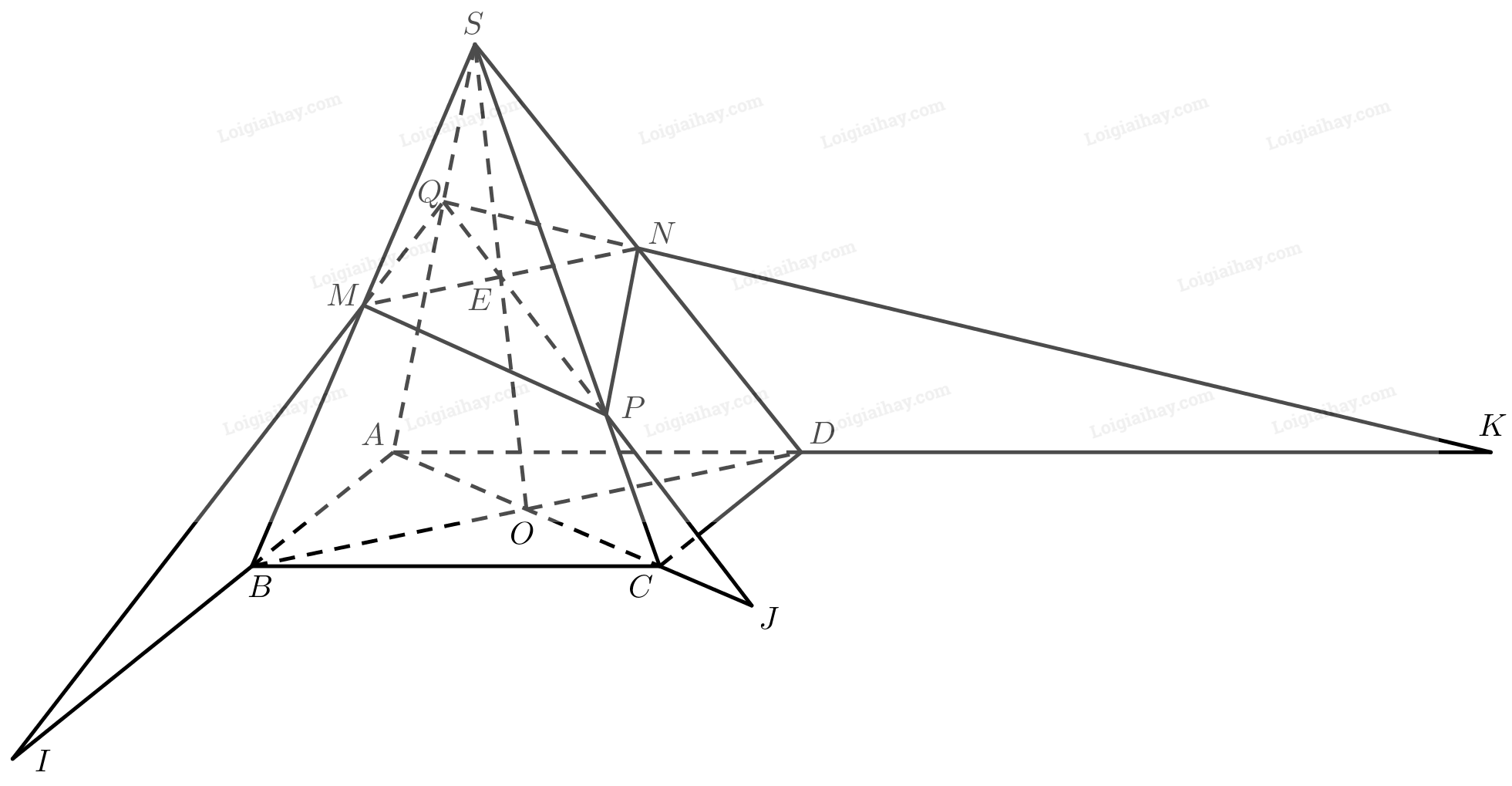
a) Gọi \(E\) là giao điểm của \(SO\) và \(MN\). Ta có:

\(\left. \begin{array}{l}E \in MN \subset \left( {MNP} \right)\\E \in S{\rm{O}}\end{array} \right\} \Rightarrow E = S{\rm{O}} \cap \left( {MNP} \right)\)

b) Gọi \(Q\) là giao điểm của \(SA\) và \(EP\). Ta có:

\(\left. \begin{array}{l}Q \in EP \subset \left( {MNP} \right)\\Q \in S{\rm{A}}\end{array} \right\} \Rightarrow Q = S{\rm{A}} \cap \left( {MNP} \right)\)

c) Ta có:

\(\begin{array}{l}\left. \begin{array}{l}I \in QM \subset \left( {MNP} \right)\\I \in AB \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow I \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\\left. \begin{array}{l}J \in QP \subset \left( {MNP} \right)\\J \in AC \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow J \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\\left. \begin{array}{l}K \in QN \subset \left( {MNP} \right)\\K \in AD \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow K \in \left( {MNP} \right) \cap \left( {ABCD} \right)\end{array}\)

Do đó, \(I,J,K\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {ABCD} \right)\).

Vậy \(I,J,K\) thẳng hàng.