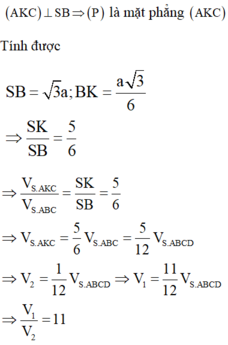Cho hình chóp S.ABCD có SA=a, SB=2a, SC=3a, A S B ^ = B S C ^ = 60 ° , C S A ^ = 90 ° . Gọi α là góc giữa hai đường thẳng SA và BC. Tính cos α.
A. cos α = 7 7
B. cos α = - 7 7
C. cos α = 0
D. cos α = 2 3
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho hình chóp S.ABCD có S A = a , S B = 2 a , S C = 3 a và A S B ⏜ = A S C ⏜ = B S C ⏜ = 60 o . Biết đáy ABCD là hình bình hành. Tính thể tích V của khối chóp S.ABCD.
A. V = a 3 2
B. V = a 3 2 2
C. V = a 3 2 3
D. V = 3 a 3 2
Chọn đáp án A
Áp dụng công thức
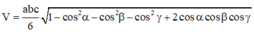
![]()
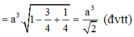
Suy ra V S . A B C D = a 2 2 ( đ v t t )
Cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = 2a, SC = 3a. Khoảng cách từ điểm S đến mặt phẳng (ABC) là
A. 5 a 6
B. 6 a 7
C. 7 a 6
D. 6 a 5
Cho hình chóp S.ABCD có đáy là hình vuông cạnh, tam giác SAB cân tại S. SA=SB=2a, (SAB) \(\perp\) (ABCD)
a, Tính (SD,(ABCD))
b, (SH, (SCD)) với H là trung điểm của
c, (SC, (SAB))
d, (SA, (SBC))
Cho hình chóp S. ABC có các góc tại đỉnh S cùng bằng 60 0 , SA = a, SB = 2a, SC = 3a . Tính khoảng cách từ đỉnh A đến mặt phẳng (SBC).
![]()
![]()
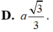
Cho hình chóp S.ABC có các góc tại đỉnh S cùng bằng 60 ° , S A = a , S B = 2 a , S C = 3 a . Tính khoảng cách từ đỉnh A đến mặt phẳng (SBC)
A. a 3
B. a 6
C. a 6 3
D. a 3 3
Chọn C.
Phương pháp: Sử dụng công thức tính thể tích khối chóp khi biết ba góc ở một đỉnh và ba cạnh ở đỉnh đó.
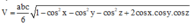
(trong đó a, b, c là độ dài ba cạnh, x, y, z là số đo ba góc ở một đỉnh)
Sau đó tính khoảng cách dựa vào công thức tính thể tích h = 3 V h .
Cách giải: Áp dụng công thức trên ta có:
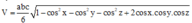
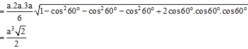

Cho hình chóp S.ABC có các góc tại đỉnh S cùng bằng 600, SA = a, SB = 2a, SC = 3a. Tính khoảng cách từ đỉnh A đến mặt phẳng (SBC)
![]()
![]()
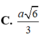
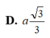
Cho hình chóp S.ABCD có A S B ^ = C S B ^ = 60 ° , A S C ^ = 90 ° , S A = S B = a , S C = 3 a Tính thể tích của khối chóp S.ABCD
A. a 3 2 4
B. a 3 6 18
C. a 3 2 12
D. a 3 6 6
Chọn A
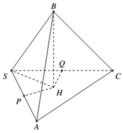 Gọi P,Q lần lượt là hình chiếu vuông góc của B lên SA; SC
Gọi P,Q lần lượt là hình chiếu vuông góc của B lên SA; SC
Kẻ B H ⊥ ( A B C )
Ta có
· ![]()
![]()
· ![]()
· ![]()
Suy ra tứ giác SPHQ là hình vuông :
![]()
Trong
∆
S
H
B
vuông tại H: 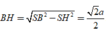
Vậy ![]()
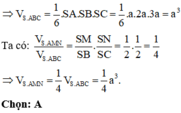
Cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau và S A = a , S B = 2 a , S C = 3 a . Gọi M, N lần lượt là trung điểm của các cạnh SB, SC. Tính theo a thể tích hình chóp S.AMN.
A. a 3 4 .
B. 3 a 3 4 .
C. a 3 2 .
D. a 3
Phương pháp:
+) Thể tích của tứ diện vuông có độ dài các cạnh góc vuông là a, b, c là: V = 1 6 a b c
+) Sử dụng công thức tỉ số thể tích Simpson
Cách giải:
S.ABC là tứ diện vuông tại đỉnh S
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh bằng a, A B C ^ = 60 0 , SA=SB=SC, SD= 2a. Gọi (P) là mặt phẳng qua A và vuông góc với SB tại K. Mặt phẳng (P) chia khối chóp S.ABCD thành hai phần có thể tích V 1 ; V 2 trong đó V 1 là thể tích khối đa diện chứa đỉnh S. Tính V 1 V 2
A. 11
B. 7
C. 9
D. 4
Đáp án A
Trong mặt phẳng dựng đường thẳng đi qua A và vuông góc vưới SB tại K
Ta chứng minh được