Cho a, b, c là các số thực và z = − 1 2 + 3 2 i . Giá trị của a + b z + c z 2 a + b z 2 + c z bằn
A. a + b + c.
B. a 2 + b 2 + c 2 − a b − b c − c a .
C. a 2 + b 2 + c 2 + a b + b c + c a .
D. 0
PB
Những câu hỏi liên quan
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn
(
x
+
3
)
2
+
(
y
-
2
)
2
+
(
z
+
1
)...
Đọc tiếp
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn ( x + 3 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 2 và a+b+c=1. Giá trị nhỏ nhất của biểu thức P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 là
A. 3 - 2
B. 3 + 2
C. 5 - 2 6
D. 5 + 2 6
cho hàm số \(\dfrac{-x+2}{x-1}\) có đồ thị (C) và điểm A(a;1) . Gọi S là tập hợp tất cả các giá trị thực củ tham số a để có đúng 1 tiếp tuyến của (C) đi qua A. Tổng tất cả các giá trị của S là
\(y'=\dfrac{-1}{\left(x-1\right)^2}\)
Gọi phương trình đường thẳng d qua A có dạng: \(y=k\left(x-a\right)+1\)
d tiếp xúc (C) khi và chỉ khi hệ sau có nghiệm:
\(\left\{{}\begin{matrix}\dfrac{-x+2}{x-1}=k\left(x-a\right)+1\\\dfrac{-1}{\left(x-1\right)^2}=k\end{matrix}\right.\)
\(\Rightarrow\dfrac{-x+2}{x-1}=\dfrac{-\left(x-a\right)}{\left(x-1\right)^2}+1\)
\(\Leftrightarrow\left(x-2\right)\left(x-1\right)=x-a-\left(x-1\right)^2\)
\(\Leftrightarrow2x^2-6x+3=-a\) (1)
Để có đúng 1 tiếp tuyến qua A khi (1) có đúng 1 nghiệm
\(\Rightarrow y=-a\) tiếp xúc \(y=2x^2-6x+3\)
\(\Leftrightarrow-a=-\dfrac{3}{2}\Rightarrow a=\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
Cho số phức z thỏa mãn |z - 1 + 3i|+|z + 5 + i| 2
65
Giá trị nhỏ nhất của |z + 2 + i| đạt được khi z a + bi với a,b là các số thực dương. Giá trị của
2
a
2
+
b
2
bằng A. 17 B. 33 C. 24 D. 36
Đọc tiếp
Cho số phức z thỏa mãn
|z - 1 + 3i|+|z + 5 + i| = 2 65 Giá trị nhỏ nhất của
|z + 2 + i| đạt được khi z = a + bi với a,b là các số thực dương. Giá trị của 2 a 2 + b 2 bằng
A. 17
B. 33
C. 24
D. 36
Cho số phức z thỏa mãn
z
-
1
+
3
i
+
z
¯
+
5
+
i
2
65
. Giá trị nhỏ nhất của
z
+
2
+
i...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 + 3 i + z ¯ + 5 + i = 2 65 . Giá trị nhỏ nhất của z + 2 + i đạt được khi z = a + b i với a, b là các số thực dương. Giá trị của 2 b + 3 a bằng
A. 19
B. 16
C. 24
D. 13
Chọn đáp án B.
Cách 1: (Sử dụng kiến thức Hình học)
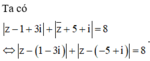
Gọi M, A, B, I lần lượt là điểm biểu diễn cho các số phức
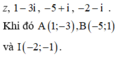
Có I là trung điểm của đoạn thẳng AB và
Áp dụng bất đẳng thức Cô-si, ta có
Cách 2: (Sử dụng kiến thức Đại số)
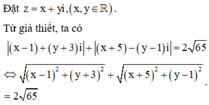
Áp dụng bất đẳng thức Bu-nhi-a-cốp-xky, ta có
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
z
-
1
+
3
i
+
z
¯
+
5
+
i
2
65
Giá trị nhỏ nhất của
z
+
2
+
i...
Đọc tiếp
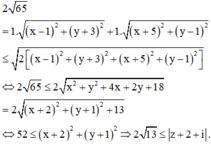
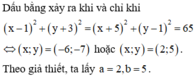
Cho số phức z thỏa mãn z - 1 + 3 i + z ¯ + 5 + i = 2 65 Giá trị nhỏ nhất của z + 2 + i đạt được khi z = a + b i với a,b là các số thực dương. Giá trị của 2 a 2 + b 2 bằng
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn
(
x
+
1
)
2
+
(
y
+
1
)
2
+...
Đọc tiếp
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 4 và a + b + c = 6 . Tính giá trị nhỏ nhất của P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 . .
Cho số phức
z
x
+
y
i
với x, y là các số thực không âm thỏa mãn
z
-
3
z
-
1
+
2
i
và biểu thức
P
z
2
-
z
-...
Đọc tiếp
Cho số phức z = x + y i với x, y là các số thực không âm thỏa mãn z - 3 z - 1 + 2 i và biểu thức P = z 2 - z - 2 + i z 2 - z - 2
z 1 - i + z - 1 + i . Giá trị lớn nhất và giá trị
nhỏ nhất của P lần lượt là:
A. 0 và - 1
B. 3 và - 1
C. 3 và 0
D. 2 và 0
Cho số phức zx+yi với x, y là các số thực không âm thỏa mãn
z
-
3
z
-
1
+
2
i
1
và biểu thức
P
z
2
-...
Đọc tiếp
Cho số phức z=x+yi với x, y là các số thực không âm thỏa mãn z - 3 z - 1 + 2 i = 1 và biểu thức P = z 2 - z - 2 + i ( z 2 - z - 2 ) z ( 1 - i ) + z ¯ ( 1 + i ) . Giá trị lớn nhất và giá trị nhỏ nhất của P lần lượt là:
A. 0 và -1
B. 3 và -1
C. 3 và 0
D. 2 và 0
Cho số phức z = a+bi(a,b ϵ ℝ) thỏa mãn |z|=5z và z(2+i)(1-2i) là một số thực. Tính giá trị P=|a|+|b|
A.P=8
B.P=4
C.P=5
D. P=7
1) Với x, y, z là các số thực thỏa mãn xy + yz + zx 13, chứng minh rằng 21x^2+21y^2+z^2ge782) Cho các số thực x, y, z khác 0 thỏa mãn x + y + z 3xyz, chứng minh rằngfrac{3}{x^2}+frac{1}{y^2}+frac{3}{z^2}ge63) Với a, b, c là các số thực dương thỏa mãn a + b + c 3, tìm giá trị nhỏ nhất của P a3 + 64b3 + c3
Đọc tiếp
1) Với x, y, z là các số thực thỏa mãn xy + yz + zx = 13, chứng minh rằng \(21x^2+21y^2+z^2\ge78\)
2) Cho các số thực x, y, z khác 0 thỏa mãn x + y + z = 3xyz, chứng minh rằng\(\frac{3}{x^2}+\frac{1}{y^2}+\frac{3}{z^2}\ge6\)
3) Với a, b, c là các số thực dương thỏa mãn a + b + c = 3, tìm giá trị nhỏ nhất của P = a3 + 64b3 + c3
1) \(21x^2+21y^2+z^2\)
\(=18\left(x^2+y^2\right)+z^2+3\left(x^2+y^2\right)\)
\(\ge9\left(x+y\right)^2+z^2+3.2xy\)
\(\ge2.3\left(x+y\right).z+6xy\)
\(=6\left(xy+yz+zx\right)=6.13=78\)
Dấu "=" xảy ra <=> x = y ; 3(x+y) = z; xy + yz + zx= 13 <=> x = y = 1; z= 6
2) \(x+y+z=3xyz\)
<=> \(\frac{1}{xy}+\frac{1}{yz}+\frac{1}{zx}=3\)
Đặt: \(\frac{1}{x}=a;\frac{1}{y}=b;\frac{1}{z}=c\)=> ab + bc + ca = 3
Ta cần chứng minh: \(3a^2+b^2+3c^2\ge6\)
Ta có: \(3a^2+b^2+3c^2=\left(a^2+c^2\right)+2\left(a^2+c^2\right)+b^2\)
\(\ge2ac+\left(a+c\right)^2+b^2\ge2ac+2\left(a+c\right).b=2\left(ac+ab+bc\right)=6\)
Vậy: \(\frac{3}{x^2}+\frac{1}{y^2}+\frac{3}{z^2}\ge6\)
Dấu "=" xảy ra <=> a = c = \(\sqrt{\frac{3}{5}}\); \(b=2\sqrt{\frac{3}{5}}\)
khi đó: \(x=z=\sqrt{\frac{5}{3}};y=\sqrt{\frac{5}{3}}\)