Với a > 0,b > 0 thì a b + a b b a bằng:
A. 2
B. 2 a b b
C. a b
D. 2 a b
CMR với mọi a,b,c thực thì
A) a^2+b^2+c^2+ab+Bc+ca lớn hơn hoặc bằng 0
B)a^2+b^2+c^2-ab-bc-ca lớn hơn hoặc băng 0
ta áp dụng cô-si la ra
a^2+b^2+c^2 ≥ ab+ac+bc
̣̣(a - b)^2 ≥ 0 => a^2 + b^2 ≥ 2ab (1)
(b - c)^2 ≥ 0 => b^2 + c^2 ≥ 2bc (2)
(a - c)^2 ≥ 0 => a^2 + c^2 ≥ 2ac (3)
cộng (1) (2) (3) theo vế:
2(a^2 + b^2 + c^2) ≥ 2(ab+ac+bc)
=> a^2 + b^2 + c^2 ≥ ab+ac+bc
dấu = khi : a = b = c
Bạn cm hộ mình cô si la dc k mình chưa học đến
A= a^2/bc +b^2/ac +c^2/ab
a,b,c khác 0, a+b+c=0
A=? ( A không bằng 0 và 2( cái kết quả này mình bấm thì sai rồi))
a)Chứng minh rằng với mọi a và b thì
a^4 - 2a^3b+2a^2b^2 - 2ab^3+ b^4 lớn hơn hoăc bằng 0
b) Cho a^2 = b^2+c^2. Chứng minh rằng (5a - 3b+ 4c)(5a - 3b - 4c) lớn hơn hoặc bằng 0
Cho a cộng b bằng 6 . Tìm a và b sao cho a nhân b lớn nhất ( a,b khác 0 và a nhỏ hơn b )
- Nếu a bằng 1 thì b bằng 6 trừ …………bằng ………, khi đó a nhân b bằng ……………
_ nếu a bằng 2 thì b bằng 6 trừ ……… , khi đó a nhân b bằng ………
_ nếu a bằng 3 thì ………………………………………
Vậy với a bằng…………, b bằng …………… thì a nhân b lớn nhất
nếu a bằng 1 thì b bằng 6 trừ 1 bằng 6 , khi đó a nhân b bằng 6
nếu a bằng 2 thì b bằng 6 trừ 2 bằng 6 , khi đó a nhân b bằng 8
nếu a bằng 3 thì b bằng 6 trừ 3 bằng 6 , khi đó a nhân b bằng 9
vậy với a bằng 2 , b bằng 4 thì a nhân b lớn nhất
ta k chọn a bằng 3 , b bằng 3 vì lúc này a = b k được tính
xin loi minh viet nham a=2 b=4
......1.....1......5
..........2...2.....8
......3 thì b = 6-3,khi do a.b=9
......2....4....
Chứng minh rằng với a+b>c và |a-b|<c với a,b,c >0 thì phương trình bậc hai a^2x^2 +(a^2+b^2-c^2)x +b^2=0 vô nghiệm
ĐOẠN MK BÔI ĐỎ GIẢI THÍCH HỘ
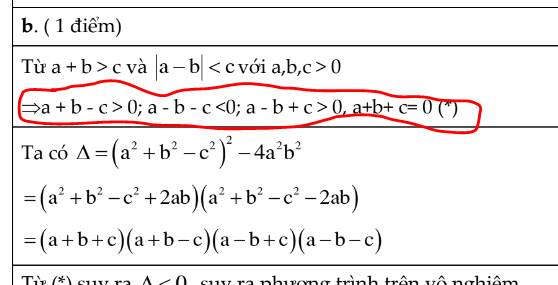
Lời giải:
Từ $a+b> c\Rightarrow a+b-c>0$ (cái này hiển nhiên)
Từ $|a-b|< c\Leftrightarrow |a-b|^2< c^2$
$\Leftrightarrow (a-b)^2< c^2$
$\Leftrightarrow (a-b-c)(a-b+c)<0$
Với $c>0$ thì $a-b-c< a-b+c$ nên để tích âm thì $a-b-c<0< a-b+c$
Hay $a-b-c<0$ và $a-b+c>0$
Bài 1: Cho A= x(x-4). Với giá trị nào của x thì: A=0; A<0; A>0
Bài 2: Cho B= (x-3) : x (x khác 0). Với giá trị nào của x thì: B=0 ; B<0; B>0
Chỉ mình ạ! \(a^2>b\) ; \(a^2< b\) .
* Xét từng trường hợp b<0 , b=0 , b>0.
* Còn a thì sao ạ có các trường hợp như trên không giải thích!
* Nếu mà đang lớn hơn, nhỏ hơn thêm dấu bằng vào thành lớn hơn hoặc bằng, nhỏ hơn hoặc bằng thì nó có bị thay đổi gì không. Nếu có thì giải thihs giúp mình ạ!
--------------------------------------------------
\(a^2\ge b^2\) và \(a^2\le b^2\) có giống tương tự như bài trên hay không giải tích giúp mình ạ! Nếu khác các bạn lại viết rõ ra nhé!
* Ngoài ra các anh chị học nhiều hiểu rộng hơn rồi còn những công thức nào như trên liệt kê ra giúp mình trong các trường hợp giải bài tập nhé ạ! Em cảm ơn ạ!
* Giups mình chi tiết nhá!
Em không nêu ra yêu cầu và các điều kiện liên quan của đề bài thì làm sao mn giúp em được?
camcon :
Ví dụ như của em: Giải bất phương trình $x^2>4$.
Ta đưa về dạng 1 vế chứa 0 như sau:
$x^2>4$
$\Leftrightarrow x^2-4>0$
$\Leftrightarrow (x-2)(x+2)>0$
Đến đây ta có 2 TH xảy ra:
TH1: \(\left\{\begin{matrix} x-2>0\\ x+2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x>2\\ x>-2\end{matrix}\right.\Rightarrow x>2\)
TH2: \(\left\{\begin{matrix} x-2< 0\\ x+2< 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x< 2\\ x< -2\end{matrix}\right.\Rightarrow x< -2\)
Vậy tóm lại $x>2$ hoặc $x< -2$
cho biểu thức p=\(\left(\dfrac{b-a}{\sqrt{b}-\sqrt{a}}-\dfrac{a\sqrt{a}-b\sqrt{b}}{a-b}\right):\dfrac{\left(\sqrt{b}-\sqrt{a}\right)^2+\sqrt{ab}}{\sqrt{a}+\sqrt{b}}\)với a lớn hơn bằng 0,b lớn hơn bằng 0,a khác b
a rút gọn p
b cm p lớn hơn bằng 0
a)
\(P=\left(\dfrac{b-a}{\sqrt{b}-\sqrt{a}}-\dfrac{a\sqrt{a}-b\sqrt{b}}{a-b}\right):\dfrac{\left(\sqrt{b}-\sqrt{a}\right)^2+\sqrt{ab}}{\sqrt{a}+\sqrt{b}}\)
\(=\left[\sqrt{b}+\sqrt{a}-\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(a+\sqrt{ab}+b\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\right]:\dfrac{b-\sqrt{ab}+a}{\sqrt{a}+\sqrt{b}}\)
\(=\left(\sqrt{b}+\sqrt{a}-\dfrac{a+\sqrt{ab}+b}{\sqrt{a}+\sqrt{b}}\right).\dfrac{\sqrt{a}+\sqrt{b}}{a-\sqrt{ab}+b}\)
\(=\dfrac{\left(\sqrt{a}+\sqrt{b}\right)^2-a-\sqrt{ab}-b}{\sqrt{a}+\sqrt{b}}.\dfrac{\sqrt{a}+\sqrt{b}}{a-\sqrt{ab}+b}\)
\(=\dfrac{\sqrt{ab}}{\sqrt{a}+\sqrt{b}}.\dfrac{\sqrt{a}+\sqrt{b}}{a-\sqrt{ab}+b}\)\(=\dfrac{\sqrt{ab}}{a-\sqrt{ab}+b}\)
b) \(P=\dfrac{\sqrt{ab}}{a-\sqrt{ab}+b}=\dfrac{\sqrt{ab}}{\left(\sqrt{a}-\dfrac{1}{2}\sqrt{b}\right)^2+\dfrac{3}{4}b}\)
Vì \(\left(\sqrt{a}-\dfrac{1}{2}\sqrt{b}\right)^2+\dfrac{3}{4}b>0;\forall a\ge0;b\ge0;a\ne b\)
\(\sqrt{ab}\ge0\)\(\forall a\ge0;b\ge0\)
\(\Rightarrow P=\dfrac{\sqrt{ab}}{\left(\sqrt{a}-\dfrac{1}{2}\sqrt{b}\right)^2+\dfrac{3}{4}b}\ge0\)
Vậy...
Chứng minh đẳng thức:
a) \(\dfrac{\sqrt{a}}{\sqrt{a}-\sqrt{b}}-\dfrac{\sqrt{a}}{\sqrt{a}+\sqrt{b}}-\dfrac{2b}{a-b}=\dfrac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
( với a > hoặc bằng 0; b > hoặc bằng 0; a khác b )
a: \(=\dfrac{a+\sqrt{ab}-a+\sqrt{ab}-2b}{a-b}\)
\(=\dfrac{2\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)}{a-b}\)
\(=\dfrac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
CMR với số thực a,B,c,d,e thì a^2+b^2+c^2+d^2+e^2 lớn hơn hoặc bằng 0