Hoạt động 3
a) Với mỗi số thực a, so sánh \(\sqrt {{a^2}} \) và \(\left| a \right|\); \(\sqrt[3]{{{a^3}}}\) và a
b) Cho a, b là hai số thực dương. So sánh: \(\sqrt {a.b} \) và \(\sqrt a .\sqrt b \)
a: \(\sqrt{a^2}=\left|a\right|\)
\(\sqrt[3]{a^3}=a\)
b: \(\sqrt{a\cdot b}=\sqrt{a}\cdot\sqrt{b}\)
Cho biết hai số thực a và b có tổng bằng 3.
Khẳng định nào sau đây là đúng về tích của hai số a và b?
A. Có giá trị nhỏ nhất là 9 4
B. Có giá trị lớn nhất là 9 4
C. Có giá trị lớn nhất là 3 2
D. Không có giá trị lớn nhất.
Vì a + b = 3 nên b = 3 - a . Do đó:
a b = a 3 - a = - a 2 + 3 a = - a 2 - 2 . 3 2 a + 9 4 + 9 4 = - a - 3 2 2 + 9 4 ≤ 9 4 ∀ a
a b = 9 4 ⇔ a = b = 3 2 Vậy giá trị lớn nhất của a.b là 9 4 (đạt được khi a = b = 3 2 ).
Đáp án là B.
Cho a, b là hai số thực dương và m, n là hai số thực tùy ý. Khẳng định nào sau đây sai?
A. a m b m = a b m
B. a m . a n = a m . n
C. a m n = a m . n
D. 1 b − n = b n
Xác định tính đúng sai của mỗi mệnh đề sau:
a) Nếu \(2a - 1 > 0\) thì \(a > 0\) (a là số thực cho trước).
b) \(a - 2 > b\) nếu và chỉ nếu \(a > b + 2\) (a, b là hai số thực cho trước).
a) Mệnh đề có dạng \(P \Rightarrow Q\) với P: “\(2a - 1 > 0\)” và Q: “\(a > 0\)”
Ta thấy khi P đúng (tức là \(a > \frac{1}{2}\)) thì Q cũng đúng. Do đó, \(P \Rightarrow Q\) đúng.
b) Mệnh đề có dạng \(P \Leftrightarrow Q\) với P: “\(a - 2 > b\)” và Q: “\(a > b + 2\)”
Khi P đúng thì Q cũng đúng, do đó, \(P \Rightarrow Q\) đúng.
Khi Q đúng thì P cũng đúng, do đó, \(Q \Rightarrow P\) đúng.
Vậy mệnh đề \(P \Leftrightarrow Q\) đúng.
Cho hai số thực a và b với 1 < a < b . Chọn khẳng định đúng.
program sosanh;
uses crt;
var a,b,c : real;
begin
readln(a,b);
c:= a-b;
if c>0 then writeln(' a lon hon b');
if c<0 then writeln('a nho hon b');
if c=0 then writeln('a bang b');
readln;
end.
Dốt tin nên chỉ làm dc vậy, đúng thì 5 sao nhé
Cho hai số thực a và b a < b sao cho ∫ a b 3 + 2 x − x 2 d x đạt giá trị lớn nhất. Tìm b − a .
A. 2
B. 4
C. 6
D. 8
Đáp án B.
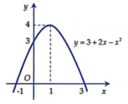
Bảng xét dấu:
Từ bảng xét dấu, dễ thấy ∫ a b 3 + 2 x − x 2 d x lớn nhất khi a = − 1 và b = 3 , tức là b − a = 4
Cho hai số phức z = a + b i và z ' = a ' + b ' i ( a , b , a ' , b ' ∈ R ) Số phức z z ' có phần thực là
