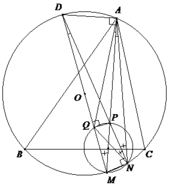
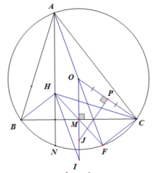
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O.
Gọi M là một điểm trên cung nhỏ B C ⏜ (M khác B; C và AM không đi qua O).
Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.
1). Gọi D là điểm đối xứng với điểm M qua O. Chứng minh rằng ba điểm N, P, D thẳng hàng.
2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.