Có bao nhiêu giá trị m nguyên dương để hệ phương trình m x − y = 3 2 x + m y = 9 có nghiệm duy nhất (x,y) sao cho biểu thức A = 3 x - y nhận giá trị nguyên
A. 4
B. 2
C. 3
D. 1
Cho hệ phương trình: \(\left\{{}\begin{matrix}mx+4y=10-m\\x+my=4\end{matrix}\right.\)
a) Xác định các giá trị nguyên m để hệ có nghiệm duy nhất (x ; y) sao cho x > 0, y > 0.
b) Tìm giá trị nguyên m để hệ có nghiệm (x ; y) với x ; y là số nguyên dương.
Giải hệ phương trình: \(\left\{{}\begin{matrix}mx+4y=10-m\\x+my=4\end{matrix}\right.\)
a) Xác định các giá trị nguyên m để hệ có nghiệm duy nhất (x ; y) sao cho x > 0, y > 0.
b) Tìm giá trị nguyên m để hệ có nghiệm (x ; y) với x ; y là số nguyên dương.
a) Với \(m=0\) ta có:
\(\left\{{}\begin{matrix}0x+4y=10-0\\x+0y=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=\dfrac{5}{2}\end{matrix}\right.\) (nhận trường hợp này).
Với \(m\ne0\), ta có:
\(\left\{{}\begin{matrix}mx+4y=10-m\\x+my=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}mx+4y=10-m\\-mx-m^2y=-4m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(4-m^2\right)y=10-5m\left(1\right)\\x+my=4\left(2\right)\end{matrix}\right.\)
Biện luận:
Với \(m=2\) \(\left(1\right)\Rightarrow0y=0\) (phương trình vô số nghiệm),
Với \(m=-2\Rightarrow0y=20\) (phương trình vô nghiệm).
Với \(m\ne\pm2\Rightarrow y=\dfrac{10-5m}{4-m^2}=\dfrac{5\left(2-m\right)}{\left(2-m\right)\left(2+m\right)}=\dfrac{5}{m+2}\)
Vì \(y>0\Rightarrow\dfrac{5}{m+2}>0\Leftrightarrow m+2>0\Leftrightarrow m>-2\)
Thay \(y=\dfrac{5}{m+2}\) vào (2) ta được:
\(x+\dfrac{5m}{m+2}=4\Leftrightarrow x=\dfrac{8-m}{m+2}\)
Vì x>0 \(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}8-m>0\\m+2>0\end{matrix}\right.\\\left\{{}\begin{matrix}8-m< 0\\m+2< 0\end{matrix}\right.\end{matrix}\right.\Rightarrow-2< m< 8\)
Vì m là số nguyên và \(m\ne2\) nên \(m\in\left\{-1;0;1;3;4;5;6;7\right\}\)
Vậy \(m\in\left\{1;0;1;3;4;5;6;7\right\}\) thì hệ đã cho có nghiệm duy nhất sao cho \(x>0,y>0\).
b) Với \(m=0\) ta có nghiệm \(\left(x;y\right)=\left(4;\dfrac{5}{2}\right)\) (loại).
Với \(m=2\). Ta có hệ vô số nghiệm với nghiệm tổng quát có dạng \(\left\{{}\begin{matrix}x\in R\\y=2-\dfrac{x}{2}\end{matrix}\right.\)
Vì y là số nguyên dương nên:
\(\left\{{}\begin{matrix}x⋮2\\2-\dfrac{x}{2}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x⋮2\\x< 4\end{matrix}\right.\). Mặt khác x>0.
\(\Rightarrow x=2\Rightarrow y=1\)
Với \(m\ne\pm2\). Ta có \(y=\dfrac{5}{m+2}\).
Vì x,y là các số nguyên dương nên x,y>0. Nên:
\(m\in\left\{-1;0;1;3;4;5;6;7\right\}\) (1')
Mặt khác: \(5⋮\left(m+2\right)\)
\(\Rightarrow m+2\inƯ\left(5\right)\)
\(\Rightarrow m+2\in\left\{1;-1;5;-5\right\}\)
\(\Rightarrow m\in\left\{-1;-3;3;-7\right\}\) (2')
Từ (1') ,(2') \(\Rightarrow m\in\left\{-1;3\right\}\)
Vậy \(m\in\left\{-1;2;3\right\}\) thì hệ có nghiệm \(\left(x;y\right)\) với x,y là số nguyên dương.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [0;2018] để hệ phương trình x - y + m = 0 x y + y = 1 có nghiệm?
A. 2016
B. 2018
C. 2019
D. 2017
Cho hệ phương trình 2 m + 1 x + y = 2 m − 2 m 2 x − y = m 2 − 3 m . Với m ≠ − 1 và m ∈ Z . Có bao nhiêu giá trị của m để hệ phương trình có nghiệm nguyên?
A. 1
B. 3
C. 2
D. 4
Ta có: D = 2 m + 1 1 m 2 − 1 = − 2 m − 1 − m 2 = − m + 1 2
D x = 2 m − 2 1 m 2 − 3 m − 1
= − 2 m + 2 − m 2 + 3 m = − m 2 + m + 2 = m + 1 2 − m
D y = 2 m + 1 2 m − 2 m 2 m 2 − 3 m = 2 m + 1 m 2 − 3 m − m 2 2 m − 2
= − 3 m 2 − 3 m = − 3 m m + 1
Nếu m ≠ − 1 thì hệ phương trình có nghiệm duy nhất
x = D x D = m − 2 m + 1 = 1 − 3 m + 1 y = D y D = 3 m m + 1 = 3 − 3 m + 1
Để x , y ∈ Z suy ra 3 m + 1 ∈ Z , m + 1 ∈ U , ( 3 ) = ± 1 ; ± 3
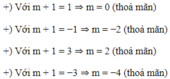
Vậy có 4 giá trị của m thoả mãn đề bài.
Đáp án cần chọn là: D
Có bao nhiêu giá trị m nguyên dương để phương trình log 3 ( x - 3 ) - log 9 x 2 = log 3 ( m - 9 ) có nghiệm?
A. 9
B. 10
C. Vô số.
D. 0
Điều kiện: x > 3 m > 0
Phương trình tương đương với:
![]()
![]()
Vì 0 < x - 3 3 = 1 - 3 x < 1 , ∀ x ∈ 3 ; + ∞ do đó phương trình có nghiệm
⇔ 0 < m - 9 < 1 ⇔ 9 < m < 10 . Vì vậy không có số nguyên nào thoả mãn.
Chọn đáp án D.
Cho hệ phương trình ( x+y = 2 mx−y = m với m là tham số.
a) Giải hệ phương trình khi m = −2.
b) Tìm giá trị của m để hệ phương trình có nghiệm duy nhất (x; y) sao cho 3x−y = −10.
c) Tìm giá trị nguyên của m để hệ phương trình có nghiệm (x; y) mà x, y là những số nguyên
a) Với m = -2
=> hpt trở thành: \(\left\{{}\begin{matrix}x+y=2\\-2x-y=-2\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}y=2-x\\-x=0\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\)
Vậy S = {0; 2}
b) Ta có: \(\left\{{}\begin{matrix}x+y=2\left(1\right)\\mx-y=m\left(2\right)\end{matrix}\right.\)
=> x + mx = 2 + m
<=> x(m + 1) = 2 + m
Để hpt có nghiệm duy nhất <=> \(m\ne-1\)
<=> x = \(\dfrac{m+2}{m+1}\) thay vào pt (1)
=> y = \(2-\dfrac{m+2}{m+1}=\dfrac{2m+2-m-2}{m+1}=\dfrac{m}{m+1}\)
Mà 3x - y = -10
=> \(3\cdot\dfrac{m+2}{m+1}-\dfrac{m}{m+1}=-10\)
<=> \(\dfrac{2m+6}{m+1}=-10\) <=> m + 3 = -5(m + 1)
<=> 6m = -8
<=> m = -4/3
c) Để hpt có nghiệm <=> m \(\ne\)-1
Do x;y \(\in\) Z <=> \(\left\{{}\begin{matrix}\dfrac{m+2}{m+1}\in Z\\\dfrac{m}{m+1}\in Z\end{matrix}\right.\)
Ta có: \(x=\dfrac{m+2}{m+1}=1+\dfrac{1}{m+1}\)
Để x nguyên <=> 1 \(⋮\)m + 1
<=> m +1 \(\in\)Ư(1) = {1; -1}
<=> m \(\in\) {0; -2}
Thay vào y :
với m = 0 => y = \(\dfrac{0}{0+1}=0\)(tm)
m = -2 => y = \(\dfrac{-2}{-2+1}=2\)(tm)
Vậy ....
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình cos 2 x + m sin x - m = 0 có nghiệm?
A. 0
B. 1
C. 2
D. vô số
Đáp án B
PT

Đặt
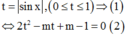
Để (1) có nghiệm thì (2) có nghiệm ![]() có nghiệm
có nghiệm ![]()
Suy ra 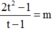 có nghiệm
có nghiệm ![]()
Xét hàm số 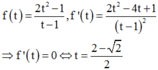
Lập bảng biến thiên hàm số 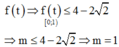
Có bao nhiêu giá trị nguyên dương của m < 20 để bất phương trình log 2 x 2 + 2 3 x 2 + 4 x + m ≤ x 2 + 4 x + m - 5 có nghiệm ∀ x ∈ R .
A. 15.
B.12
C.14
D.13
Có bao nhiêu giá trị nguyên dương của m < 20 để bất phương trình log 2 x 2 + 2 3 x 2 + 4 x + m ≤ x 2 + 4 x + m - 5 có nghiệm ∀ x ∈ ℝ .
A. 15
B. 12
C. 14
D. 13