Số phức z = –4 + 3i được biểu diễn bởi điểm M có tọa độ
A. M (4;–3)
B. M (–4;3)
C. M (3;–4)
D. M (4;3)
PB
Những câu hỏi liên quan
Số phức z=-4+3i được biểu diễn bởi điểm M có tọa độ
A. M(4;-3)
B. M(-4;3)
C. M(3;-4)
D. M(4;3)
Đáp án B
Phương pháp:
Điểm biểu diễn của số phức 
là M(a;b)
Cách giải:
Số phức z=-4+3i được biểu diễn bởi điểm M có tọa độ M(-4;3)
Đúng 0
Bình luận (0)
Số phức z = -4 + 3i được biểu diễn bởi điểm M có tọa độ
Trên mặt phẳng tọa độ, số phức
z
3
i
-
4
được biểu diễn bởi điểm A,B,C,D? A. Điểm D B. Điểm B C. Điểm A D. Điểm C
Đọc tiếp
Trên mặt phẳng tọa độ, số phức z = 3 i - 4 được biểu diễn bởi điểm A,B,C,D?
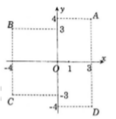
A. Điểm D
B. Điểm B
C. Điểm A
D. Điểm C
Trên mặt phẳng tọa độ, số phức z 3i - 4 được biểu diễn bởi điểm A, B, C, D? A. Điểm D B. Điểm B C. Điểm A D. Điểm C
Đọc tiếp
Trên mặt phẳng tọa độ, số phức z = 3i - 4 được biểu diễn bởi điểm A, B, C, D?
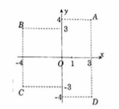
A. Điểm D
B. Điểm B
C. Điểm A
D. Điểm C
Cho số phức z thỏa mãn:
z
1
+
2
i
-
z
¯
2
-
3
i
-
4
+
12
i
. Tìm tọa độ điểm M biểu diễn số phức z. A.
M
3
;
1...
Đọc tiếp
Cho số phức z thỏa mãn: z 1 + 2 i - z ¯ 2 - 3 i = - 4 + 12 i . Tìm tọa độ điểm M biểu diễn số phức z.
A. M 3 ; 1
B. M 3 ; - 1
C. M - 1 ; 3
D. M 1 ; 3
Cho số phức z thỏa mãn:
z
(
1
+
2
i
)
-
z
¯
(
2
-
3
i
)
-
4
+
12
i
. Tìm tọa độ điểm M biểu diễn số phức z.
Đọc tiếp
Cho số phức z thỏa mãn: z ( 1 + 2 i ) - z ¯ ( 2 - 3 i ) = - 4 + 12 i . Tìm tọa độ điểm M biểu diễn số phức z.
Cho số phức
z
(
2
-
3
i
)
(
4
-
i
)
3
+
2
i
. Tìm tọa độ điểm biểu diễn của số phức z trên mặt phẳng Oxy A. . B. . C. . D. .
Đọc tiếp
Cho số phức z = ( 2 - 3 i ) ( 4 - i ) 3 + 2 i . Tìm tọa độ điểm biểu diễn của số phức z trên mặt phẳng Oxy
A. 
.
B. 
.
C. 
.
D. 
.
Cho số phức z thỏa mãn (2 - i)z = (2 + i)(1 - 3i). Gọi M là điểm biểu diễn của z. Khi đó tọa độ điểm M là.
A. M(3;1)
B. M(3;-1)
C. M(1;3)
D. M(1;-3)
Đáp án B
Dùng CASIO rút gọn z = 2 + i 1 - 3 i 2 - i = 3 - i → M 3 ; - 1 .
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn (2-i)z = (2+i)(1-3i). Gọi M là điểm biểu diễn của z. Khi đó tọa độ điểm M là.
A. M(3;1)
B. M(3;-1)
C. M(1;3)
D. M(1;-3)
Đáp án B
Dùng CASIO rút gọn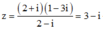 
=> M(3;-1)
Đúng 0
Bình luận (0)