Đáp án B
Dùng CASIO rút gọn 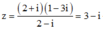
=> M(3;-1)
Đáp án B
Dùng CASIO rút gọn 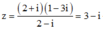
=> M(3;-1)
Gọi M là điểm biểu diễn của số phức z thỏa mãn 3| z + i| = | 2 z ¯ - z + 3i | . Tập hợp tất cả những điểm M như vậy là
A. một parabol.
B. một đường thẳng.
C. một đường tròn.
D. một elip.
Cho số phức z thỏa mãn: z ( 1 + 2 i ) - z ¯ ( 2 - 3 i ) = - 4 + 12 i . Tìm tọa độ điểm M biểu diễn số phức z.
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn 30 i 1 - z = 9 - 3i. Gọi M là điểm biểu diễn số phức z. Tìm tung độ của M
A. 2
B. 3
C. -3
D. -1
Cho số phức z thỏa mãn z + 3 i + z - 3 i = 10 . Gọi M 1 ; M 2 lần lượt là điểm biểu diễn số phức z có môđun lớn nhất và nhỏ nhất. Gọi M là trung điểm của M 1 M 2 , M(a, b) biểu diễn số phức w, tổng a + b nhận giá trị nào sau đây?
A. 7 2
B. 5
C. 4
D. 9 2
Gọi M là điểm biểu diễn số phức z thỏa mãn 1 - i z - 1 + 5 i = 0 . Tọa độ của M là
A. (-2; 3)
B. (3; -2)
C. (-3; 2)
D. (-3; -2)
Cho số phức z thỏa mãn iz + 2 - i = 0. Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ Oxy đến điểm M(3;-4) là:
A. 2 5
B. 13
C. 2 10
D. 2 2
Tìm điểm M biểu diễn bởi số phức z thỏa mãn z = (2+3i)(i+1)
A. M(2;3)
B. M(3;4)
C. M(-1;5)
D. M(5;5)
Trong mặt phẳng phức Oxy, các số phức z thỏa mãn z + 2 i - 1 = z + i . Mô dul của số phức z được biểu diễn bởi điểm M sao cho MA ngắn nhất với A(1;3) là
A. 10
B. 7
C. 2 3
D. 2 5
Cho số phức z thỏa mãn (3+i)z = 13 - 9i. Tìm tọa độ của điểm M biểu diễn z.
A. M = (-3;4)
B. M = (3;-4)
C. M = (-3;-4)
D. M = (1;-3)