Giúp bài 4 vs ạ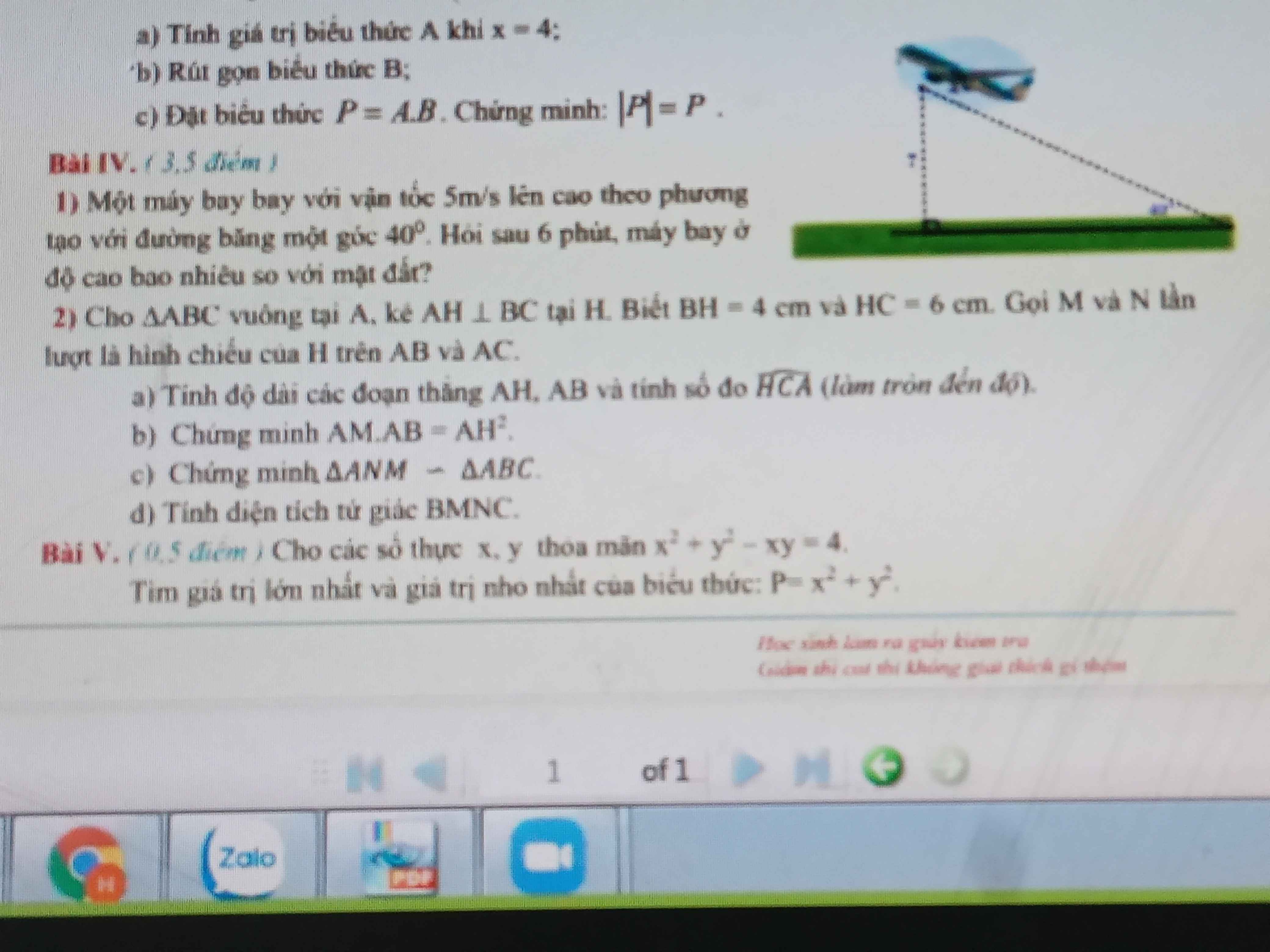
H24
Những câu hỏi liên quan

Giúp mình bài 3a vs 4 vs ạ
bài 3 :
gọi số xe ban đầu của đội là x(xe)(x>2)
sau khi 2 xe điều động đi làm viêc khác thì số xe còn lại là x-2(xe)
theo dự định cả đôi xe phải vận chuyển 120 tấn hàng
nên mỗi xe ban đầu phải vận chuyển:120/x(tấn hàng)
mỗi xe lúc sau( khi có 2 xe bị điều động đi chỗ khác) phải chuyển
120/x-2(tấn hàng)
vì để hoàn thành công việc mỗi xe còn lại phải chở thêm 2 tấn hàng
=>pt:(120/x-2)-120/x=2
giải pt theo \(\Delta\) ta tìm được x1=12(thỏa mãn)
x2=-10(loại)
vậy lúc đầu trong đội có 12 xe
Đúng 1
Bình luận (0)
Câu 4:
a) Xét ΔOAB có OA=OB(=R)
nên ΔOAB cân tại O(Định nghĩa tam giác cân)
Ta có: ΔOAB cân tại O(cmt)
mà OI là đường trung tuyến ứng với cạnh đáy AB(I là trung điểm của AB)
nên OI là đường cao ứng với cạnh AB(Định lí tam giác cân)
hay OI\(\perp\)AB
Ta có: \(\widehat{OIM}=90^0\)(OI\(\perp\)AB)
nên I nằm trên đường tròn đường kính OM(1)
Ta có: \(\widehat{OCM}=90^0\)(gt)
nên C nằm trên đường tròn đường kính OM(2)
Ta có: \(\widehat{ODM}=90^0\)(gt)
nên D nằm trên đường tròn đường kính OM(3)
Từ (1), (2) và (3) suy ra O,I,C,M,D cùng nằm trên một đường tròn(Đpcm)
Đúng 0
Bình luận (0)
Giúp e bài 4 vs ạ(có vẽ hình),e cần cách lm dễ hiểu chi tiết,bài này e cần lắm luôn đó ạ nên giúp e lm đúng vs(nếu mn có thời gian thì giúp e luôn bài 2 vs,e ko đc chắc chắn bài này e lm có đúng ko)e cảm ơn nhìu lắm ạ!!!
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
Đúng 1
Bình luận (0)
giúp mik bài 3 và bài 4 vs ạ

Bài 4:
a: Xét tứ giác ANBH có
M là trung điểm của AB
M là trung điểm của NH
Do đó: ANBH là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên ANBH là hình chữ nhật
Đúng 0
Bình luận (0)
giúp bài 4 vs ạ
Đọc tiếp
giúp bài 4 vs ạ
b:
Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}3x+5=\dfrac{1}{4}x-6\\y=3x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{11}{4}x=-11\\y=3x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=-7\end{matrix}\right.\)
Thay x=-4 và y=-7 vào y=2x+b, ta được:
b-8=-7
hay b=1
Đúng 0
Bình luận (0)

Giúp mình bài 4 vs ạ
Câu 1:
1.
a. $2x-4=0$
$\Leftrightarrow x=2$
b. $x^2-5x+4=0$
$\Leftrightarrow (x-1)(x-4)=0$
$\Rightarrow x-1=0$ hoặc $x-4=0$
$\Leftrightarrow x=1$ hoặc $x=4$
2.
\(\left\{\begin{matrix} 2x+y=1\\ x-3y=4\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2x+y=1\\ 2x-6y=8\end{matrix}\right.\)
\(\Rightarrow 7y=-7\) (trừ theo vế 2 PT)
$\Leftrightarrow y=-1$
$x=4+3y=4+3(-1)=1$
Đúng 1
Bình luận (0)
Câu 2.
1.
\(P=\left[\frac{(\sqrt{a}+1)(\sqrt{a}+2)}{(\sqrt{a}+2)(\sqrt{a}-1)}-\frac{\sqrt{a}(\sqrt{a}+1)}{(\sqrt{a}+1)(\sqrt{a}-1)}\right]:\frac{2\sqrt{a}}{(\sqrt{a}-1)(\sqrt{a}+1)}\)
\(=\left(\frac{\sqrt{a}+1}{\sqrt{a}-1}-\frac{\sqrt{a}}{\sqrt{a}-1}\right).\frac{(\sqrt{a}-1)(\sqrt{a}+1)}{2\sqrt{a}}=\frac{1}{\sqrt{a}-1}.\frac{(\sqrt{a}-1)(\sqrt{a}+1)}{2\sqrt{a}}=\frac{\sqrt{a}+1}{2\sqrt{a}}\)
2.
Để \(P=\frac{\sqrt{a}+1}{2\sqrt{a}}=\frac{2\sqrt{a}-1}{4}\)
\(\Leftrightarrow 4(\sqrt{a}+1)=2\sqrt{a}(2\sqrt{a}-1)=4a-2\sqrt{a}\)
\(\Leftrightarrow 4a-6\sqrt{a}-4=0\)
\(\Leftrightarrow 2a-3\sqrt{a}-2=0\Leftrightarrow (\sqrt{a}-2)(2\sqrt{a}+1)=0\)
\(\Rightarrow \sqrt{a}=2\Leftrightarrow a=4\) (thỏa ĐKXĐ)
Đúng 1
Bình luận (0)
Câu 3.
1.
PT hoành độ giao điểm:
$(m-3)x+16-(x+m^2)=0$
$\Leftrightarrow (m-4)x=m^2-16(*)$
Để $(d),(d')$ cắt nhau tại 1 điểm trên trục tung thì PT $(*)$ nhận $x=0$ là nghiệm.
Điều này xảy ra khi $m=\pm 4$
Với $m=4$ thì $(d)\equiv (d')$ (loại). Do đó $m=-4$
2.
\(\Delta'=(m-2)^2+m^2=2m^2-4m+4=2(m-1)^2+2>0\)với mọi $m\in\mathbb{R}$ nên pt luôn có 2 nghiệm pb với mọi $m\in\mathbb{R}$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=2(2-m)\\ x_1x_2=-m^2\end{matrix}\right.\)
Vì $x_1x_2=-m^2\leq 0$ mà $x_1<x_2$ nên:
$|x_1|=-x_1; |x_2|=x_2$. Do đó:
$|x_1|-|x_2|=6$
$\Leftrightarrow -x_1-x_2=6$
$\Leftrightarrow 2(2-m)=-6$
$\Leftrightarrow m=5$
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
giúp mik bài 4 vs ạ 
 giúp mình bài 4 vs ạ
giúp mình bài 4 vs ạ
Giúp em bài 4 vs ạ
b4 bạn tham khảo:
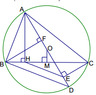
* Chứng minh các tứ giác ABHF và BMFO nội tiếp.
- Từ giả thiết suy ra: 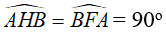
=> H và F thuộc đường tròn đường kính AB (quỹ tích cung chứa góc)
Vậy tứ giác ABHF nội tiếp đường tròn đường kính AB
- M là trung điểm của BC (gt), suy ra: OM ⊥ BC
Khi đó: 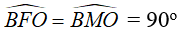
Nên M, F thuộc đường tròn đường kính OB(quỹ tích cung chứa góc).
Vậy tứ giác BMOF nội tiếp đường tròn đường kính OB
* Chứng minh HE // BD.
Dễ chứng minh tứ giác ACEH nội tiếp đường tròn đường kính AC.
Đúng 4
Bình luận (0)
Giúp mình bài 4 vs ạ




